Capítulo10 Credibilidade e racionalidade sequencial
10.2 Racionalidade sequencial e indução reversa
Nós já vimos que podemos usar a indução reversa para achar os únicos equilíbrios e Nash que demandam racionalidade dos jogadores dentro e fora do caminho de equilíbrio. Em outras palavras, os jogadores precisam jogar racionalmente em todo conjunto de informação. Chamamos esse princípio de racionalidade sequencial, pois implica que as jogadoras estão jogando racionalmente em cada estágio da sequência do jogo, seja dentro ou fora do caminho de equilíbrio.
Contudo, quando o jogo é de informação imperfeita, não podemos aplicar a indução reversa para achar jogadas sequencialmente racional. Além disso, jogos que não são finitos tambpouco podem se beneficiar da indução reversa. Caso em que é mais vantajoso usar uma formalização desenvolvida por Selten (1975) de subjogo próprio (frequentemente chamada apenas de subjogo).
10.3 Subjogo
Subjogo de um jogo extensivo com informação perfeita
Um subjogo é qualquer parte de um jogo na forma extensiva que satisfaz as seguintes condições:
- Sempre se inicia em um único nó de decisão
- Não está em um nó terminal
- Contém todos os nós que se seguem após ele
Em um jogo de informação imperfeita, acrescentamos:
- Se contiver qualquer nó de um conjunto de informação, ele conterá todos os nós do conjunto de informação.
Nós chamamos de subjogo próprio todos os subjogos que não são a árvore do jogo na sua totalidade.
Definição: Um subjogo próprio \(G\) de um jogo na forma extensiva \(\Gamma\) consiste apenas de um nó e todos os seus sucessores em \(\Gamma\) com a propriedade que se \(x \in G\) e \(x' \in h(x)\) então \(x' \in G\).
10.4 Equilíbrio de Nash Perfeito de Subjogo
A ideia é que iremos demandar que as jogadores joguem racionalmente em sequência em cada subjogo do jogo na forma extensiva. E chamaremos a isso de equilíbrio de Nash perfeito de subjogo.
Fato: em jogos de informação perfeita finitos, os equilíbrios que sobrevivem a indução reversa são equilíbrios de Nash perfeitos de subjogo.
Equilíbrio de Nash Perfeito em Subjogos
Definição informal: Um equilíbrio perfeito em subjogos é um perfil estratégico \(s^*\) com a propriedade de que, em nenhum subjogo, qualquer jogador \(i\) pode se sair melhor escolhendo uma estratégia diferente de \(s^*_i\), dado que todos os outros jogadores \(j\) aderem a \(s^*_j\).
Nessa definição (informal), requeremos que a estratrégia de cada jogadora seja ótima para toda história após ser a vez dela jogar, e não apenas no início do jogo, como no equlíbrio de Nash.
Todo jogo extensivo finito com informação perfeita possui (pelo menos) um equilíbrio perfeito de subjogo.
Um jogo finito significa que em nenhum momento um jogador possui infinitas opções de ações. Para dar um exemplo trivial (do Osborne): um único jogador escolhe um número menor que 1 e recebe um pagamento igual ao número que ela escolhe. Não há um número maior que todos os outros números menores que um, então o jogador único não possui uma ação ótima, e assim o jogo não possui um equilíbrio perfeito de subjogo.
10.5 Exercícios
Ache todos os subjogos do jogo abaixo.
## Loading required package: ggplot2## Want to understand how all the pieces fit together? Read R for
## Data Science: https://r4ds.hadley.nz/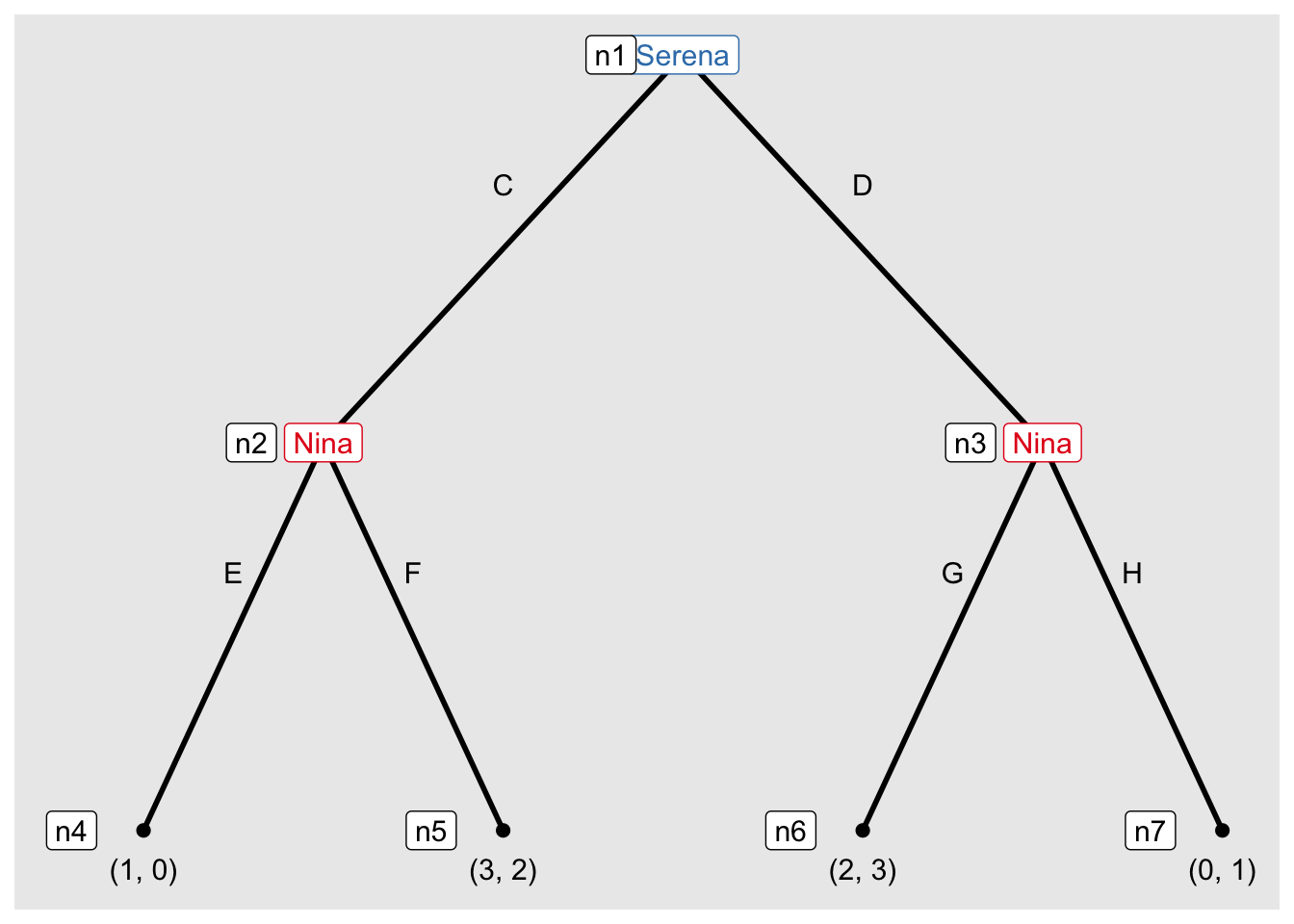
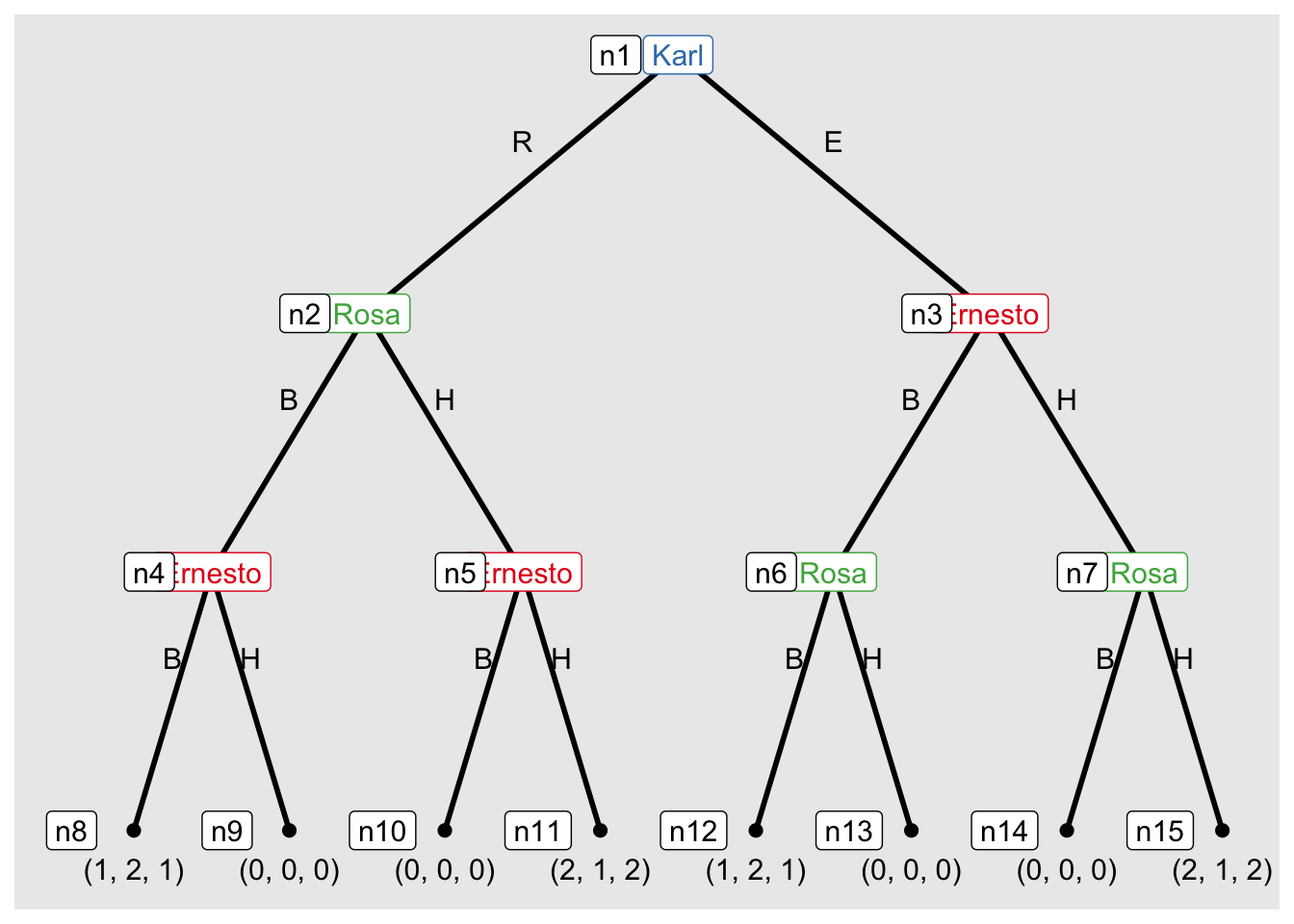
Modelo o jogo como uma árvore (forma extensiva) e ache todos os subjogos do jogo abaixo. (exercício 156.2c do Osborne).
Os políticos Rosa e Ernesto precisam tomar uma posição sobre um assunto. As opções são Berlim (B) ou Havana (H). Eles escolhem sequencialmente. Uma terceira pessoa, Karl, determina quem escolhe primeiro. Tanto Rosa quanto Ernesto se importam apenas com as ações que escolhem, não com quem escolhe primeiro. Rosa prefere o resultado em que ambos escolhem B ao resultado em que ambos escolhem H, e prefere esse resultado a qualquer um dos casos em que ela e Ernesto escolhem ações diferentes; ela é indiferente entre esses dois últimos resultados. As preferências de Ernesto diferem das de Rosa no sentido de que os papéis de B e H são invertidos. As preferências de Karl são as mesmas que as de Ernesto. Modele essa situação como um jogo extensivo com informação perfeita. (Especifique os componentes do jogo e represente o jogo em um diagrama.)
- Modele o jogo do Ultimato com três períodos e:
- conte quantos subjogos existem.
- Ache o equilíbrio de Nash Perfeito em Subjogos
- Considere um jogo de dois períodos em que um trabalhador busca emprego.No período 1, ele recebe uma oferta de um salário \(S_1\) e deve decidir se aceita ou não. Se aceitar, este é seu salário e para de procurar emprego. Caso não aceite, continua no período 2, e recebe uma oferta de salário \(S_2 > S_1\) com probabilidade \(p\) e \(0\), isto é, não recebe oferta com probabilidade \(1-p\).
- Desenho o jogo na forma extensiva.
- Calcule quantos subjogos existem.
- Suponha que \(S_2 = 2S_1\) e \(p=.8\)? Qual o equilíbrio de Nash perfeito em Subjogos do jogo.