Capítulo9 Jogos Dinâmicos

9.1 Introdução

Vamos falar de jogos din Considere novamente o jogo Bach e Stravinsky. Suponha que a jogadora 1 joga primeiro e e a jogadora 2 pode observar a esoclha de 1. Imagine que ela vai para um lugar, liga para a amiga e diz: estou aqui no lugar tal (espetáculo do Bach ou do Stravinsky).

Veja que em termos de equilíbrios de Nash, continuamos com os mesmos dois equilíbrios de antes. Porém, não faz sentido achar que o equilíbrio (S,S) será jogado, pois a jogadora 1 sabe que, se for para Bach, 2 também irá. Jogos na forma normal não capturam muito bem a noção de jogos sequenciais e racionalidade sequencial.

A forma estratégica do jogo, de fato, não traz informações nem sobre a ordem dos movimentos, nem as ações disponíveis para cada jogadora na sua vez de jogar.

Por isso, iremos alterar a representação de nosso jogo, para a forma extensiva, que tornará explícito a ordem em que as jogadoras jogam, e o que cada jogadora sabe quando é sua vez de jogar. Nesse cenário, estratégias referem-se a planos contingentes de ações (como no jogo da bandeira), em vez de ações não-contigentes.

Iremos introduzir a noção de indução reversa ou indução para trás como uma forma de solucionar jogos. Noção que for formalizada por Selten (1965) como equilíbrio de subjogo-perfeito e contempla situações em que jogadoras se movem simultaneamente em múltiplos períodos e a indução reversa não pode ser aplicada.

Comecemos então pela introdução do que significa descrever um jogo na forma extensiva.

9.2 Jogo na forma extensiva

Um jogo na forma extensiva pode ser visto como uma generalização multi-estágio de árvores de decisão.

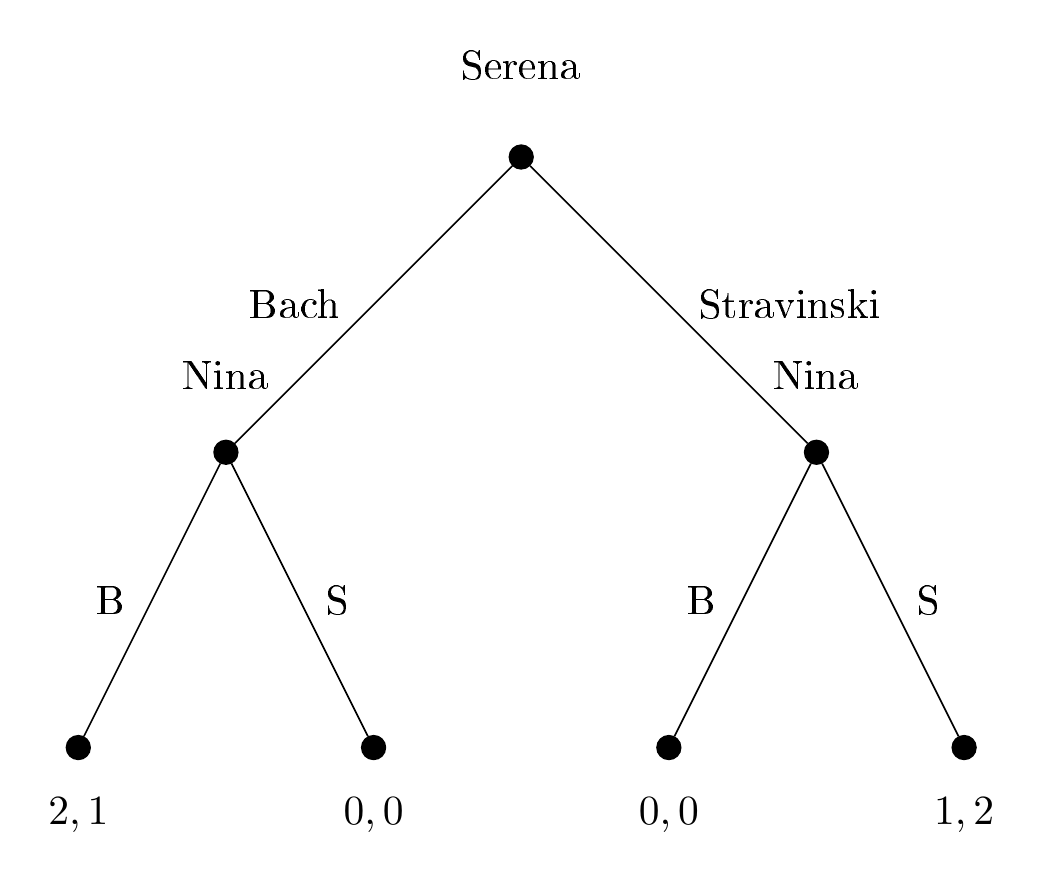
Figure 9.1: Representação do Jogo da coordenação

A árvore do jogo é lida de cima para baixo. No topo está quem joga primeiro. O retângulo com o nome da jogadora é chamado de nó. No primeiro nó, Serena tem duas ações possíveis, “Bach” e “Stravinski”. Uma vez que ela escolha sua ação, é a vez da Nina, que também tem duas opções (“bach” e “stravinsky”, em caixa baixa, para distinguir as ações das duas jogadoras). Se Serena escolheu Bach, Nina está no galho da esquerda. Se Serena escolheu Stravinsky, Nina está no galo da direita. E uma vez que Nina faça sua escolha, o jogo acaba e os payoffs finais são mostrados. O primeiro payoff é da jogadora 1, e o segundo da jogadora 2.

Assim, com a forma extensiva, temos como antes:

Número de jogadoras, $N$.
Payoffs ou funções de utilidade em função dos resultados, $\{u_i(\cdot)\}_{i \in N}$

E acrescentamos:

Ordem dos movimentos
Ações das jogadoras quando for a vez delas de se moverem.
O conhecimento que as jogadoras possuem quando é sua vez de se moverem.

O ponto 5 é importante para distinguir entre Nina joga depois da Serena de um lado, e Nina joga depois da Serena sabendo o que Serena jogou antes dela.

Por fim, mantemos uma suposição feita em nossos jogos anteriores, agora estendida aos itens 1-6, que é:

É conhecimento comum toda a estrutura do jogo representada pelos itens 1-6 para todas as jogadoras.

9.2.1 Definição de árovre de um jogo

Uma árvore do jogo é formada por um conjunto de nós $x \in X$ com uma relação de precedência $x > x'$, que significa “$x$ precede a $x'$”. Ou seja, $x$ vem antes de $x'$. Cada nó só tem um predecessor. A relação de precedência é transitiva ($x > x', x' > x'' \implies x > x''$), assimetrica $(x > x' \implies \neg (x' > x))$, isto é, $x$ precede $x'$, mas $x'$ não precede $x$, e incompleta (nem todos os pares podem ser ordenados). Há um nó especial, chamado raiz da árvore, denotada por $n_1$, que precede quaisquer outros nós $x \in X$. Nós que não precedem outros nós são chamados de nós terminais, denotados pelo conjunto $Z \subset X$. Nós terminais denotam o fim do jogo, com os payoffs associados. Cada nó $x$ que não é terminal é atribuído a um jogador $i(x)$ com o conjunto de ações $A_i(x)$, ou para natureza.

É uma definição longa, masque captura a estrutura “física” do jogo, ao mesmo tempo em que ignora as ações (escolhas) das jogadoras e o que sabem quando jogam.

9.3 Jogo da confiança

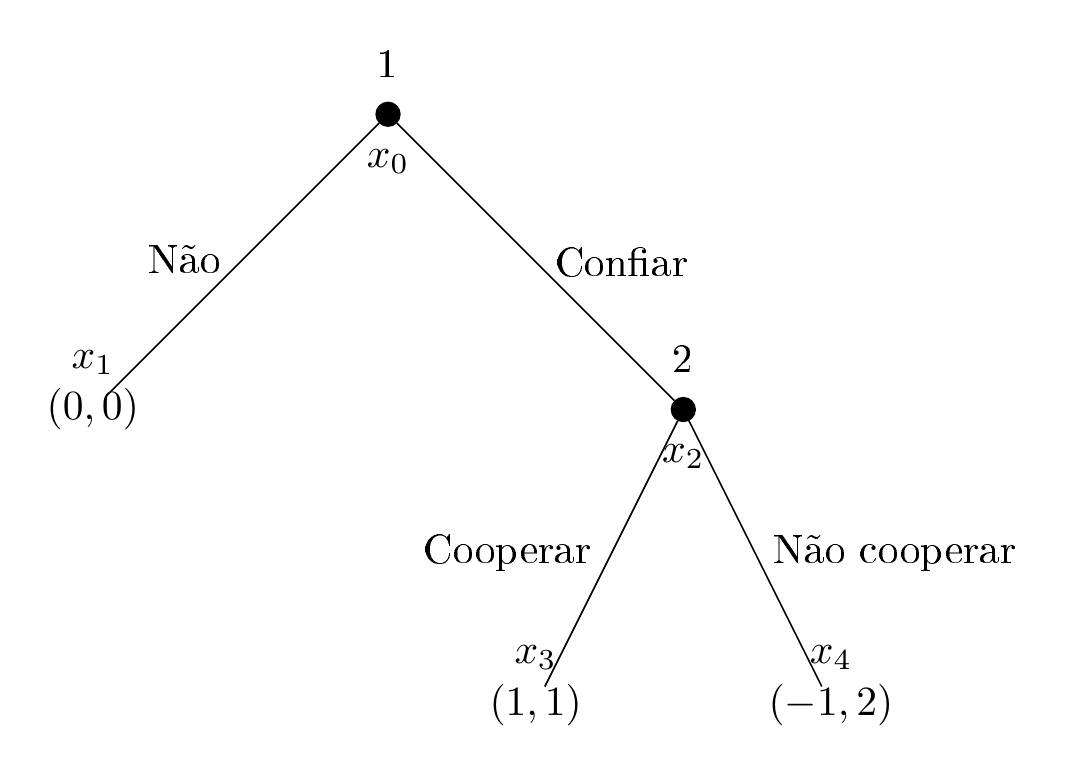
Figure 9.2: Representação do Jogo da Confiança

O jogador p1 joga primeiro. Logo, $i(n_1) = p_1$.

9.4 Informações

Quais informações cada jogador tem quando é sua vez de jogar? Uma jogadora pode ter informação bem fina sobre onde está no jogo, ou bem grosseira. Vamos então introduzir a seguinte definição:

Definição conjunto de informações:

Cada jogador $i$ tem uma coleção de conjuntos de informação $h_i$ the particiona (divide) os nós do jogo no qual uma jogadora $i$ move com as seguintes propriedades:

Se $h_i$ é uma conjunto unitário (singleton) que inclui apenas $x$, então a jogadora $i$ que se move em $x$ sabe que está em $x$.
Se $x \neq x'$ e se ambos $x \in h_i$ e $x' \in h_i$ então a jogadora $i$ que se move em $x$ não sabe se está em em $x$ ou $x'$.
Se $x \neq x'$ e se ambos $x$ e $x' \in h_i$, então $A_i(x) = A_i(x')$.

Vamos entender esta definição formal. Considere novamente o jogo do Bach e Stravinsky na forma extensiva.

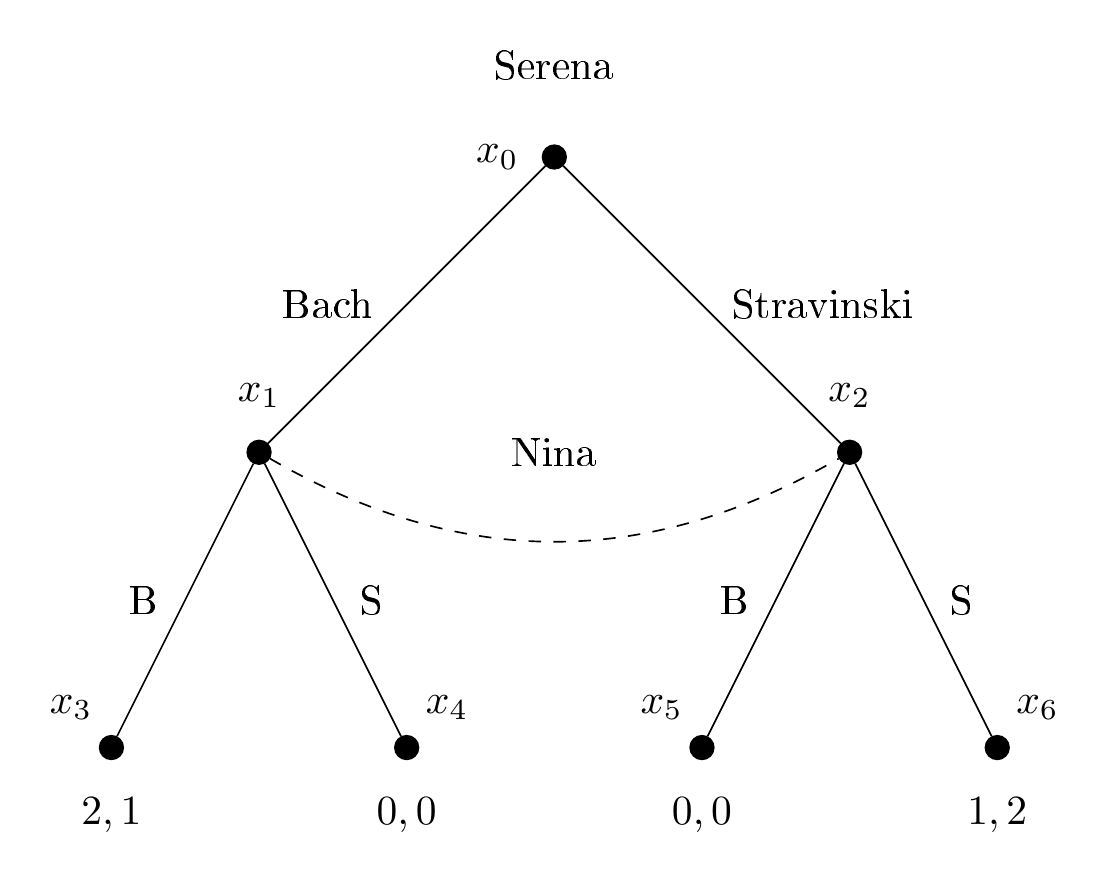
Figure 9.3: Representação do Jogo da coordenação simultâneo

No gráfico 9.1. temos $x_1$, $x_2$… como nós. Considere quando a jogadora Nina se move em $x_1$. A questão é: ela sabe que está em $x_1$? Ou não sabe se está em $x_1$ ou $x_2$? Se a gente escreve $h_2 = {x_2}$, então isso significa que o conjunto de informações em $x_1$ é um conjunto unitário. Portanto, a jogadora a jogadora possui informação que diz “estou em x_2”, que é capturado pela propriedade 1 da definição. Nesse caso, segue-se que a jogadora 2 também tem outro conjunto de informação $h_2 = {x_3}.

Se, por outro lado, Nina não sabe se está em $x_1$ ou $x_2$, como no jogo do Bach e Stravinsky simultâneo (figura 9.3), então deve ser verdade que sua informação é de que está em $x_1$ ou $x_2$, mas não sabe em qual dos dois. Nesse caso, escrevemos $h_2 = {x_1, x_2}$. Esta é a propriedade 2.

Finalmente, a propriedade 3 é essencial para manter a lógica da informação, em particular quando as ações disponíveis em cada nós forem diferentes para uma jogadora. Considere o jogo da confiança. Se ela não sabe se está no nó $x_1$ (onde o jogo terminou e não tem o que fazer) ou $x_2$, então ela não pode saber quais as ações disponíveis para ela.

Por fim, em alguns casos é possível acrescentar eventos aleatórios. Por exemplo, o jogo acima poderia ser modificado para incluir a chance de chover. Suponha que o espetáculo de Bach é a céu aberto, e o de Stravinski, não. Então, se choveu os payoffs das jogadoras é diferente de se não choveu. Vamos supor que elas preferem ficar juntas sob chuva que separadas. Como representar essa possibilidade? A forma como fazemos isso é criar uma jogadora fictícia, que é a natureza, que joga aleatoriamente sem considerações estratégicas. Essa probabilidade é exógena, no sentido de que é fixa e determinada antes do jogo começar, de modo que não depende das escolhas das jogadoras.

Eis como ficaria o jogo nesse caso:

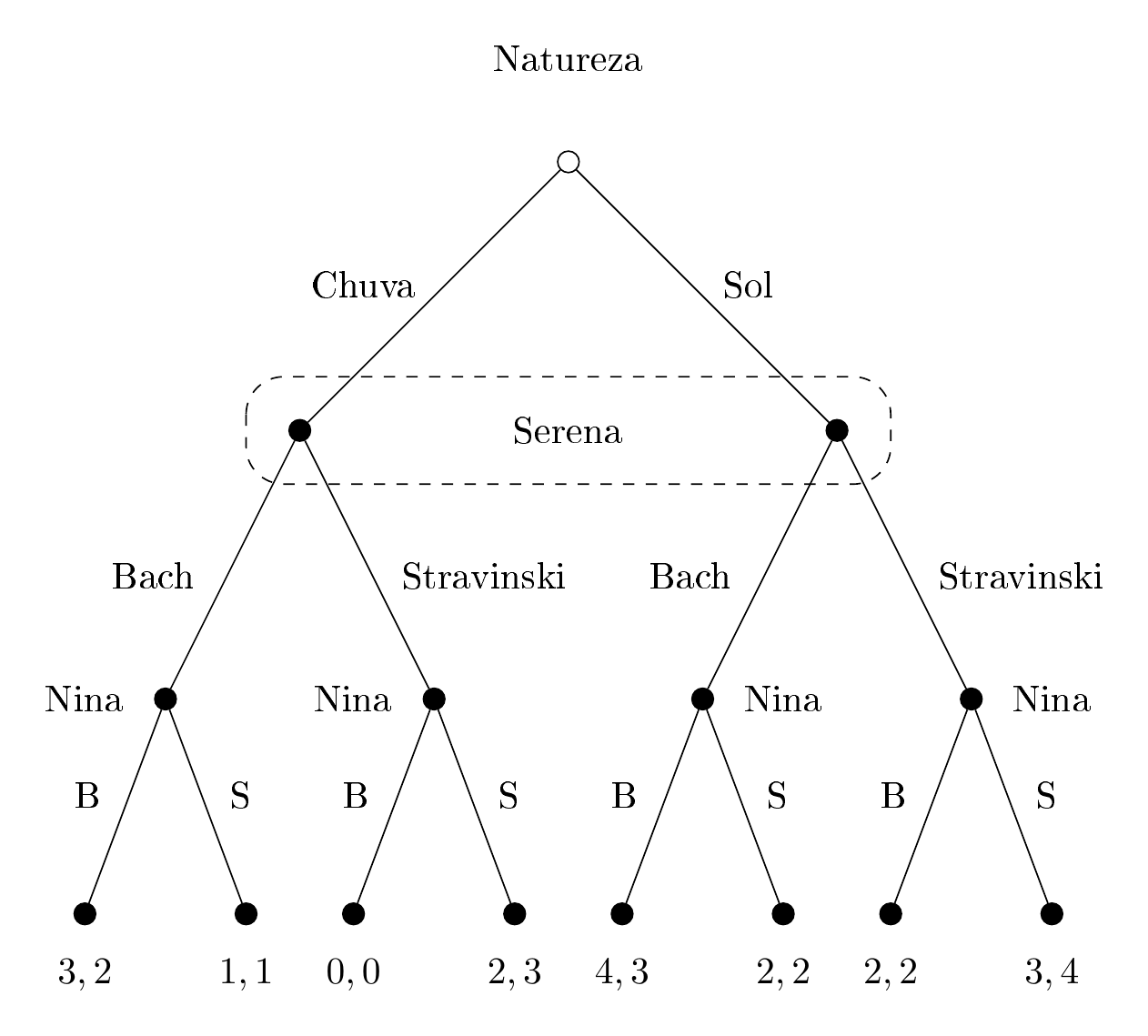
Figure 9.4: Representação do Jogo da coordenação, com a natureza movendo primerio

Na 9.4, temos algumas mudanças. O primeiro nó está representado por um círculo vazado, para indicar que é a natureza quem está jogando (e não terá um payoff). Os demais nós são representados por círculos prreenchidos, sólidos. Portanto, a natureza joga e “escolhe” se fará sol ou chuva. Na prática as leis da natureza irão operar, e podemos calcular probabilidades (no caso, 50% de chance de chover), mas a jogadorta Serena só sabeá se haverá sol ou chuva na hora do espetáculo, após ter feito sua jogada. Isso significa que Serena não sabe em qual nós está, se no da esquerda, com chuva, ou no da direita, com sol. Para indicar essa ausência de informação, é comum circularmos com uma linha tracejada os nós nos quais uma jogadora não tem informação sobre qual nó ela está. Uma vez que Serena Joga, é a vez de Nina jogar. Note que não circulamos nós de Nina com linha tracejada, de modo que isso significa que Nina sabe em qual nó está, ou seja, sabe não apenas o que Serena jogou, mas o que a natureza jogou. Como é difícil imaginar tal situação, o melhor seria indicar também que Nina não sabe o que a Natureza jogou, mas sabe o que a Serena jogou. A árovre do jogo ficartão então.

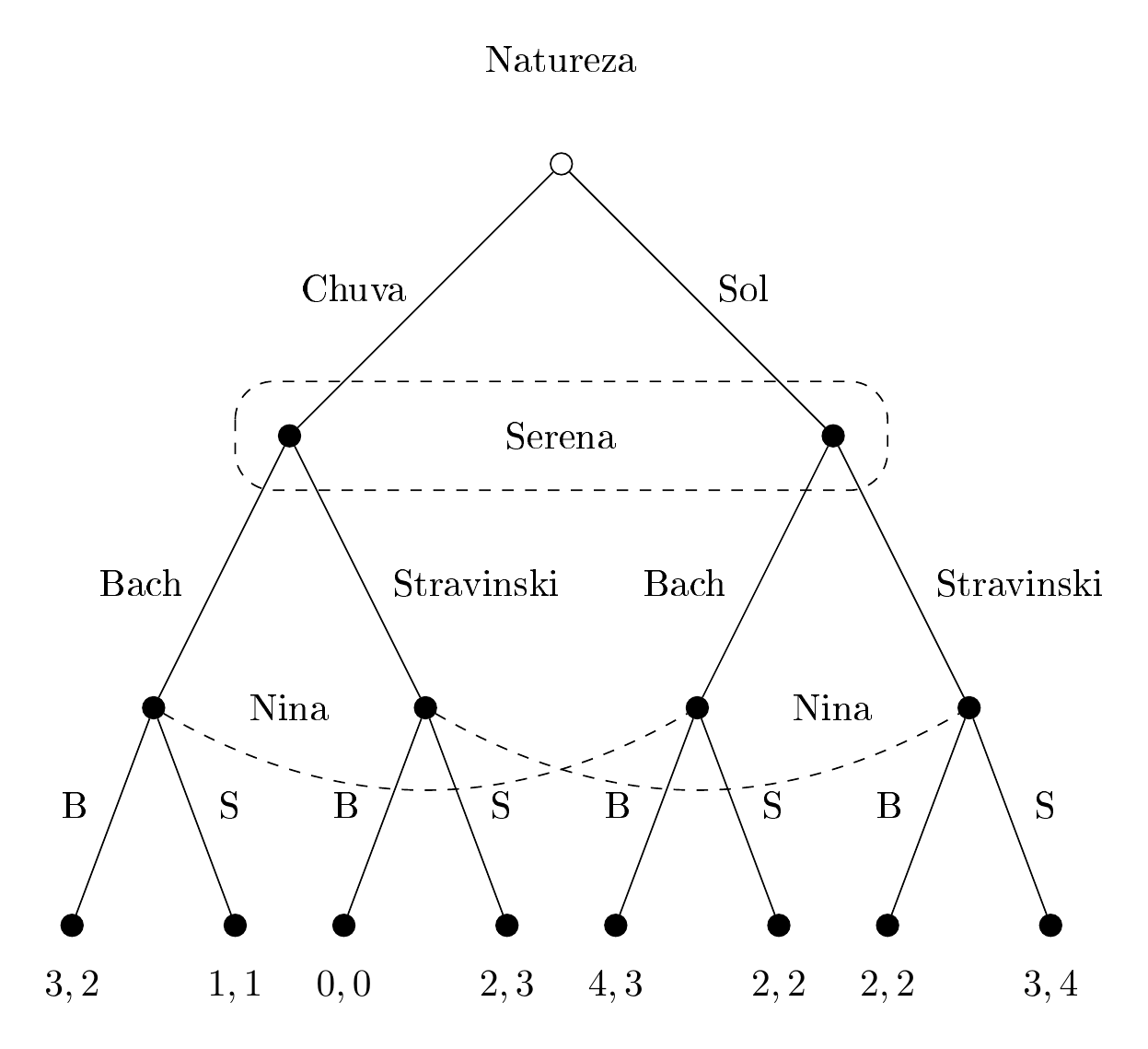
Figure 9.5: Representação do Jogo da coordenação, com a natureza movendo primerio, conjunto de informações corretos.

Nessa árvore, vale destacar dois aspectos que são diferentes da árvore anterior. Em primeiro lugar, nós descrevemos a informação completa sobre em qual nó Nina está por meio de linha tracejada curva. Poderíamos ter usado o círculo tracejado, que daria na mesma. São duas formas distintas de representar a mesma coisa e estamos incluindo aqui para fins de completude. Em segundo lugar, note os nós que estão conectados pela linha. Quando é a vez de Nina jogar, ela não sabe o que a natureza jogou, mas sabe o que Serena jogou. Isso significa que se Serena jogou “Bach”, Nina não sabe se está no ramo “Bach” com chuva ou no ramo “Bach” som sol. Similarmente, se Serena jogou “Stravinski”, Nina não sabe em qual dos dois galhos de “Stravinski” ela está. É preciso, portanto, ter cuidado quando conectar nós, pois se fizemos errado, o jogo fica completamente outro.

9.5 Jogos de informação perfeita e imperfeita

Os jogos na forma normal eram chamados de jogos de informação completa, pois todas as jogadores conheciam as ações disponíveis e as funções de payoff de todas as jogadoras, e isso era conhecimento comum.

Agora, nós temos uma situação em que uma jogadora pode ter conhecimento perfeito ou imperfeito do nó em que está, a depender do particionamento do conjunto de informações. Portanto, vale a pena distinguir entre dois tipos de jogos de informação completa.

Definição: Um jogo de informação completa no qual cada conjunto de informação é um conjunto unitário e não há jogadas da natureza é chamado um jogo de informação perfeita. Um jogo no qual pelo menos um conjunto de informação contém vários nós ou um jogo com movimentop da natureza é chamado um jogo de informação imperfeita.

9.6 Estratégias

Nós já havíamos definido uma estratégia como um plano de ação contigente. Contudo, em jogos na forma normal, essa definição era pouco útil, pois estratégias (puras) coincidiam com as ações disponíveis para as jogadoras. Na forma externsiva, a nossa definição de estratégia se revelará mais útil.

9.6.1 Estratégias puras

Consideremos novamente o jogo sequencial Bach-Stravinski na sua forma mais simples, representado pelo gráfico 9.1. Serena é a primeira a jogar e seu conjunto de informação possui apenas um nó e para ela uma estratégia pura é tão simples quanto jogar B ou S. Para Nina, a situação é um pouco mais complexa, posto que ela possui dois conjuntos de informação, um para cada estrarégia de Serena. Portanto, não basta dizer que as duas ações B e S são as estratégias de Ninas.

Estratégias Puras em Jogos na forma Extensiva: Uma estratégia pura para a jogadora $i$ é um plano completo de ação que descreve qual ação a jogadora $i$ escolherá em cada um de seus conjuntos de informação.

No jogo Bach-Stravinski 9.2, vemos que a estratégia de Serena é apenas $\{\text{Bach},\text{Stravinski}\}$, e a de nina, $\{\text{B},\text{S}\}$, pois ambas as jogadoras possuem apenas um conjunto de informação. Em outras palavras, o jogo na forma extensiva é idêntico ao jogo na forma estratégica. Já no jogo sequencial, como vimos, Nina tem dois con juntos de informação disintos no qual ela pode escolher entre duas ações (B,S), a depender de qual foi o movimento de Serena. Portanto, um plano completo de ação para Nina deve ter instruções do que fazer para cada escolha de Serena.

A escolha do conjunto de ações $\{\text{B},\text{S}\}$ deve ser contigente ao que Serena escolheu, do tipo: “Se Serena escolher Bach, escolha B”, ou “Se Serena escolher Bach, Nina escolherá S, já se Serena escolher Stravinski, Nina escolherá S” e assim por diante. Para resumir, descreveremos o conjunto de estratégias da seguinte forma:

\[ S_{\text{Nina}} = \{BB, BS, SB, SS\} \] Assim, a estratégia $BB$ quer dizer, jogue B se Serena escolher Bach, e jogue B se Serena escolher Stravinski. Por outro lado, $BS$ quer dizer, jogue B se Serena escolher Bach, e jogue S se Serena escolher Stravinski, e assim por diante. Para Serena, o conjunto de estratégias continua $S_{\text{Serena}} = \{Bach, Stravinski\}$.

Agora podemos definir formalmente o que é uma estratégia pura, se adotarmos algumas notações específicas. Seja $H_i$ a coleção de todos os conjuntos de informação no qual a jogadora $i$ joga, e seja $h_i \in H_i$ um dos conjuntos de informação de $i$. Seja $A_i(h_i)$ as ações que a jogadora $i$ pode tomar em $h_i$, e seja $A_i$ o conjunto de todas as ações da jogadora $i$, $A_i = \cup_{h_i \in H_i}A_i(h_i)$, isto é, a união de todos os elementos em todos os conjuntos $A_i(h_i)$.

Definição 9.3: Uma estratégia pura para uma jogadora $i$ é um mapeamento $s_i:H_i \rightarrow A_i$ que atribui uma ação $s_i(h_i) \in A_i(h_i)$ para todo conjunto de informação $h_i \in H_i$. Denotamos por $S_i$ o conjunto de todos os mapeamentos de estratégias puras $s_i \in S_i$.

9.6.2 Estratégias mistas

Uma estratégia mista para a jogadora $i$ é uma distribuição de probabilidade sobre suas estratégias puras $s_i \in S_i$.

Uma vez que uma estratégia mista é uma aleatorização de estratégias puras, perdemos o componente dinâmico do jogo, já que as probabilidades devem ser definidas antes do jogo começar e uma vez sorteada a estratégia a jogar, joga a escolhida independentemente da dinâmica do jogo.

No caso do jogo Bach-Strvinski, a jogadora 2 teria de aleatorizar entre (BB, BS, SB, SS). Mas não poderia ter uma estratégia do tipo, se 1 jogar “Bach”, jogo B, e se jogar “Stravinski”, jogo S com probabilidade $2/3$.

9.7 Estratégias comportamentais

Para permitir esse tipo de comportamento, definiremos o conceito de estratégia comportamental: ela especifica para cada conjunto de informação $h_i \in H_i$ uma distribuição de probabilidade independente sobre $A_i(h_i)$ e é denotada por $_i:H_i A_i(h_i), em que $\sigma_i(a_i(h_i))$ é a probabilidade que a jogadora $i$ joga a ação $a_i(h_i) \in A_i(h_i)$ no conjunto de informação $h_i$.

Pergunta: dada uma estratégia mista (não comportamental), podemos achar uma estratégia comportamental que leva ao mesmo resultado? Sim, sempre é possível fazer essa operação.

E o oposto, dada uma estratégia comportamental, podemos achar uma mista que leva ao mesmo resultado? Sim, em jogos de lembrança perfeita (perfect recall).

E um jogo é de lembrança perfeita se nenhuma jogadora jamais esquece uma informação que soube previamente.

Portanto, estratégias mistas e comportamentais são equivalentes nessas classes de jogos, no sentido de que a mesma distribuição de resultados sempre pode ser alcançada com estratégias mistas e comportamentais. Definição: perfect recall (memória perfeita)

9.8 Representação estratégica de jogos na forma extensiva

9.9 Equilíbrio de Nash e Caminhos de jogada

Como vimos, um dos equilíbrios de Nash do jogo Bach-Stravinski é (Bach, BB), e outro é (Bach, BS). E a diferença desses dois equilíbrio é o que a jogadora 2 joga no conjunto de informação fora do equilíbrio.

Vejam que na forma extensiva, cara resultado é associado a um único caminho de jogo, já que há um único caminho do nó raiz para cada nó terminal. Isso segue da definição que cada nó deve ser precedido por apenas um nó. Em termos de equilíbrio de Nash, isso significa que se um perfil de estratégia $s^{\star}$ é um equilíbrio de Nash, então cada jogadora prefere seguir o caminho predito pelo equilíbrio do que escolher outro alternativo, dado o que as demais estão fazendo. O que nos leva a mais uma definição:

Seja $\sigma^{\star} = (\sigma_1^{\star}, ..., \sigma_n^{\star})$ um perfil de estratégias comportamentais de equilíbrio de Nash em um jogo na forma extensiva. Dizemos que um conjunto de informação está no caminho de equilíbrio se dado $\sigma^{\star}$ ele é alcançado com probabilidade positiva. E dizemos que um conjunto de informação está fora do caminho de equilíbrio se dado $\sigma^{\star}$ ele nunca é alcançado.

Portanto, equilíbrios de Nash envolvem crenças do que irá ocorrer no caminho de equilíbrio e fora dele. Entretanto, deixa claro que ameaças não-críveis são aceitas pelas jogadores. Basicamente diz para jogadoras agirem racionalmente no caminho de equilíbrio, dadas as crenças dentro e fora do caminho de equilíbrio. Mas se as crenças no caminho fora de equilíbrio são importantes, agir racionalmente fora dele também deveriqa ser, certo?