Capítulo 8 - Causalidade
Até o momento estivemos estudando regressão em um sentido puramente preditivo (ou descritivo). Mas com frequência nosso interesse está em utilizar regressão para inferir causalidade. E uma regressão pode ser interpretada causalmente quando a CEF for causal. Obviamente, essa resposta é insatisfatória, pois a próxima pergunta é: quando a CEF é causal? A resposta é: A CEF é causal quando ela descreve diferenças nos resultados ponteciais (potencial outcomes) em uma dada população alvo.
Vamos então definir causalidade a partir da noção de resultados potenciais, para em seguida ver como podemos utilizar regressão para fazer inferência causal.
8.1 Resultados Potenciais
Digamos que estamos interessados em estimar o efeito causal de pertencer à base do governo sobre o percentual de votos de um deputado que será conforme indicado pelo líder do governo. Donald Rubin, em uma série de artigos nos anos 70, introduziu a noção de resultados potenciais a partir da noção mais familiar de contrafactual. Imagine um deputado que está na oposição e ele passa a fazer parte do governo. Se nós pudéssemos observar uma série de votações tanto no mundo factual em que é do governo, quando no contrafactual em que não é do governo, teríamos o efeito causal para aquele deputado de fazer parte do governo sobre seu percentual de votação em acordo com a indicação do líder do governo. Porém, não é possível observar ambos os mundos, o factual e o contrafactual ao mesmo tempo, o que é conhecido como o problema fundamental da inferência causal. Se pudéssemos observar duas terras paralelas, exatamente iguais, exceto por esse único fato, conseguiríamos calcular o efeito causal.
Seja \(Y_{1i}\) o percentual de votação potencial do deputado \(i\) quando ele é da base do governo (indicado pelo índice “1”) e seja \(Y_{0i}\) o percentual de votação potencial do deputado \(i\) quando ele não é da base do governo (indicado pelo índice “0”).
\(Y_{1i} - Y_{0i}\) é o efeito causal para \(i\) de fazer parte da base do governo e é o que gostaríamos de saber para cada deputado. Se eu pudesse observar essa diferença para cada deputado, poderia calcular o Efeito Causal Médio, \(\mathbb{E}[Y_{1i} - Y_{0i}]\), em inglês, Average Causal Effect (ACE).
Seja \(B_i\) uma variável que indica se um deputado é ou não da base do governo (\(1\) se é, \(0\) caso contrário).
O mundo factual (observado) pode ser descrito em termos dos resultados potenciais pela eqquação abaixo. É importante enfatizar que essa equação conecta os resultados observados com os resultados potenciais. Vale notar também a diferença de notação entre um resultado observado (indexado apenas o indivíduo \(i\)) e um potencial (indexado para o indivíduo \(i\) e para o tratamento potencialmente recebido).
\[\begin{equation} \tag{8.1} Y_i = Y_{0i} + (Y_{1i} - Y_{0i})*B_i \end{equation}\]
A equação nos lembra também que nós só podemos observar um dos resultados potenciais, associado a ser ou não da base do governo, mas não ambos ao mesmo tempo. Veja que se para um indivíduo \(i\) ele é da base do governo, isto é, \(B_i = 1\), então tenho para este individuo em particularque \(Y_i = Y_{1i}\), isto é, o resultado potencial coincide com o resultado observado. Essa igualdade é na verdade uma suposição, chamada de consistência.
Consistência: Essa suposição implica que o resultado potencial de um indivíduo quando recebe um tratmento é igual ao observado na realidade. Em outras palavras, consistência significa que o que você observa é o que você supunha que aconteceria se a pessoa recebesse o tratamento.
Para imaginar que consistência falhasse, imagine quando um deputado \(i\) distante ideologicamente do governo vira da base do governo ele, buscando reduzir dissonância cognitiva, muda sua ideologia para algo mais proximo do governo. Já um deputado mais alinhado não precisa fazer isso. Então, na verdade temos dois “tratamentos” acontecendo, e não um, e a hipótese de consistência não será verificada.
8.1.1 Decomposição do Efeito Causal
A equação 8.1 conecta resultados observados com resultados potenciais. Isso é particularmente útil quando quisermos estimar o efeito causal a prtir de dados observacionais. Digamos que tenho dados sobre deputados que fazem parte da base do governo e que não fazem. Nós iremos mostrar agora porque correlação (associação) não implica causalidade.
Digamos que queremos computar a média percentual de votação conforme indicação do governo para deputados da base e fora da base. Isso é dado pela equação 8.2 abaixo.
\[\begin{equation} \tag{8.2} \mathbb{E}[Y_{i}|B_i = 1] - \mathbb{E}[Y_{i}| B_i = 0] \end{equation}\]
Veja que por enquanto estamos tratando apenas de dados observados e, portanto, não podemos falar de dados potenciais. Contudo, se a suposição de consistência for válida, podemos utilizar a equação 8.1 para conectar o factual e o contrafactual.
\[\begin{equation} \begin{aligned} \mathbb{E}[Y_{i}|B_i = 1] = \mathbb{E}([Y_{0i} + (Y_{1i} - Y_{0i})*B_i)|B_i=1] \\ \mathbb{E}[Y_{i}|B_i = 1] = \mathbb{E}[(Y_{0i} + (Y_{1i} - Y_{0i})*1)|B_i=1] \\ \mathbb{E}[Y_{i}|B_i = 1] = \mathbb{E}[Y_{1i}|B_i=1] \end{aligned} \end{equation}\]
E, similarmente,
\[\begin{equation} \mathbb{E}[Y_{i}|B_i = 0] = \mathbb{E}[Y_{0i}|B_i=0] \end{equation}\]
De modo que a equação 8.2 pode ser reescrita do seguinte modo (supondo consistência):
\[\begin{equation} \mathbb{E}[Y_{i}|B_i = 1] - \mathbb{E}[Y_{i}| B_i = 0] = \mathbb{E}[Y_{1i}|B_i=1] - \mathbb{E}[Y_{0i}| B_i = 0] \end{equation}\]
Agora, podemos utilizar aquele truque de subtrair e somar a mesma coisa que não altera a equação. Em particular, somar um resultado pottencial contrafactual, isto é, o que em média um deputado que faz parte da base do governo faria se não estivesse no governo (denotado por \(Y_{0i}|B_i = 1\)). Em vermelho está o truqe matemático de subtrair e somar a mesma coisa sem alterar a equação.
\[\begin{equation} \begin{aligned} \mathbb{E}[Y_{i}|B_i = 1] - \mathbb{E}[Y_{i}| B_i = 0] = \\ \mathbb{E}[Y_{1i}|B_i=1] \color{red}{- \mathbb{E}[Y_{0i}|B_i = 1] + \mathbb{E}[Y_{0i}|B_i = 1]} - \mathbb{E}[Y_{0i}| B_i = 0] \end{aligned} \end{equation}\]
Rearranjando a equação e utilizando as propriedades do operador esperança ,temos:
\[\begin{equation} \tag{8.3} \begin{aligned} \mathbb{E}[Y_{i}|B_i = 1] - \mathbb{E}[Y_{0i}|B_i=0] = \\ \color{green}{\mathbb{E}[Y_{1i} - Y_{0i}|B_i = 1]} + \color{blue}{\mathbb{E}[Y_{0i}|B_i = 1] - \mathbb{E}[Y_{0i}| B_i = 0]} \end{aligned} \end{equation}\]
A equação 8.3 apresenta em verde o que chamamos de efeito Médio do Tratamento entre as pessoas Tratadas (em inglês, Average effect of the Treatment on the Treated, ATT) e em azul o viés de seleção. O ATT é o efeito médio porque estamos calculando a média (esperança), do efeito do Tratamento por causa do termo \(Y_{1i} - Y_{0i}\), e entre as pessoas Tratadas, isto é, que pertencem à base do governo, por que condiciona em \(B_i = 1\).
E a parte em azul é o viés de seleção porque reflete a diferença média (no percentual de votos seguindo o governo) entre as pessoas que escolheram ser da base do governo \(|B_i = 1\) e as que escolheram não ser \(|B_i = 0\) no mundo de resultados potenciais em que ambos não foram tratados (\(Y_{0i}\)). Ou seja, se pudéssemos observar o mundo contrafactual em que deputados da base estão fora do governo e computar o percentual médio de voto deles seguindo o governo, e comparar com o observado para os deputados fora da base, se houver diferença, isso é o viés de seleção.
Quando o viés de seleção é diferente de zero, então a nossa comparação ingênua da diferença média de comportamento entre governo e oposição não recupera o efeito causal médio. Por exemplo, se deputados de esquerda possuem maior chance de fazer parte do governo Lula e, pelo fato de serem mais próximos ideologicamente, tendem a votar com o governo por esse motivo, então teriam um comportamento médio diferente da oposição, mesmo se não estivessem na base do governo. Nesse exemplo, a diferença média entre governo e oposição superestima o efeito causal médio de ser da base do governo.
Esse resultado permite visualizar também porque, em um contexto experimental, podemos garantir que o viés de seleção é zero em média. Se cada pessoa é atribuída ao tratamento ou controle aleatoriamente (exemplo fictício, se der cara, é da base do governo, se der coroa, não é da base), então não há diferença média entre um grupo e outro. Obviamente, temos de supor que há compliance perfeito (isto é, um Bolsonarista alocado aleatorimnte para compor o governo deveria aceitar fazê-lo e, similarmente, um petista alocado na oposição deveria aceitar isso e serem ambos tratados assim pelo governo). Quando o compliance não é perfeito, há formas de tratar isso, mas se torna mais complicado.
Em estudos observacionais, o mecanismo de alocação de pessoas entre tratamento e controle não está sob controle do pesquisador e, portanto, não podemos garantir que o viés de seleção é zero. Em um contexto dos assim chamados experimentos naturais ou quase experimentos, a aleatorização existe, mas não é feita pelo pesquisador (caso de uma política governamental usada segundo alguma regra aleatória, como no caso do draft do Vietnam) ou a aleatorização não existe, mas é plausível supor que, para um certo subconjunto dos dados, a alocação entre tratamento e controle é como se fosse aleatório (exemplo, quando da introdução da urna eletrônica de acordo com tamanho da população, cidades com um eleitor acima do ponto de corte versus com um abaixo possui diferença aleatória em relação a, por exemplo, percentual de votos nulos. Então é possível estimar o efeito causal da urna eletrônica sobre percentual de votos nulos nesse subgrupo de cidades próximas do ponto de corte).
E em contextos mais gerais de estudos observacionais, para além de contextos quasi-experimentais, o efeito causal só pode ser recuperado (identificado) se a suposição de Conditional Independence Assumption (CIA) for válida. Essa suposição diz que, condicional a variáveis de controle, não há relação entre a alocação de tratamento e os resultados potenciais. No nosso exemplo, isso significa que, condicional a, por exemplo, a ideologia do deputado, não há correlação entre alocação para tratamento e controle e resultados potenciais. Ou seja, o viés de seleção seria zero em média. Se houver alguma variável que causa quem éselecionado (ou se seleciona) entre tratamento e controle e tmbém causa os resultados potenciais, o viés de seleção não é zero e o efeito causal não é estimável. Por exemplo, digamos que a execução de emendas parlamentares fosse diferente entre governo e oposição e que essa variável também influencia a votação. Ao não controlar para essa variável, a suposição de CIA não é atendida.
8.2 Modelo estrutural e modelo de regressão
A distinção entre CEF e CEF causal é um ponto muito importante mas no geral negligenciado. Chen & Pearl (2013), ao avaliaram livros de econometria, notaram que a maioria não fazia a distinção adequada entre modelo de regressão e modelo estrutural de regressão. Como a compreensão desse ponto é crítica para qualquer análise causal com regressão e frequentemente não feita, quero insistir nesse aspecto.
Vamos recapitular o que nós aprendemos sobre regressão e sobre causalidade.
O erro da regressão (na população) é definido como a diferença entre o \(Y\) observado e a esperança condicional \(\mathbb{E}[Y|X]\). Uma consequência dessa definição é que o erro é não correlacionado com o regressor \(X\), sejam os dados observacionais ou não.
A regressão linear pode ser jusitifcada de três modos distintos: 1. se a CEF for linear (como em um modelo saturado); 2. se queremos minimizar o erro quadrático médio das previsões; 3. é a melhor aproximação linear que existe para a CEF, seja linear ou não.
Em estudos observacionais, a análise de regressão linear identifica o modelo causal se o viés de seleção for zero. Isso requer que a suposição de indepenência (ou independência condicional) seja verdade, isto é, que a correlação entre o erro e os regressores seja zero. Ou seja, é uma suposição do modelo (e não uma propriedade ou consequência da definição do erro).
Para a suposição ser plausível, precisamos ter um modelo estrutural (como o de Resultados Potenciais) em que seja plausível (é uma suposição não testável) a independência condicional.
Muitos livros textos de regressão não diferenciam as propriedades da CEF e as suposições de um modelo estrutural (causal). Vamos ilustrar, por meio de um exemplo, o ponto de como é possível o erro da CEF ser não correlacionado com o regressor e o modelo estrutural ter erro e regressor correlacionados (e portanto a causalidade não identificada se não controlarmos para variável que garanta independência condicional.
8.2.1 Exemplo de CEF e CEF estrutural
Suponha que estou interessado em estimar o efeito causal de uma variável, que vou designar por tratamento. Meus dados são observacionais e há viés de seleção nos dados. Uma outra variável, \(X\), causa tanto o tratamento quando minha variável dependente, \(Y\). Porém, condicional a \(X\), o tratamento é independente dos resultados potenciais, ou seja, é válida a suposição de independência condicional. Vou mostrar que a o erro da CEF é independente dos regressores e, por outro lado, uma regressão sem controlar para \(X\) tem resíduo correlacionado com o regressor e, portanto, não identifica o efeito causal. Por fim, uma regressão que controle para \(X\) identifica o efeito causal.
8.3 Simulação de Resultados Potenciais e Causalidade
Vamos rodar uma simulação para ilustrar o ponto.
## potential outcomes
n1 <- 5000
tau <- 2 # ATE Average Treatment Effect (ATE) or Average Causal Effect (ACE)
alpha <- 1
eta_0 <- rnorm(n1)
eta_1 <- rnorm(n1)
##
n <- n1+n1
x <- rnorm(n1)
gamma <- 2
nu_0 <- rnorm(n1)
nu_1 <- rnorm(n1)
eta_0 <- gamma*x + nu_0
eta_1 <- gamma*x + nu_1
treatment <- rep(1:0, each=n1)
# potential outcomes
y_1 <- alpha + tau*treatment[1:n1] + eta_1
y_0 <- alpha + tau*treatment[(n1+1):n] + eta_0
# ATT ou ACE
mean(y_1 - y_0)## [1] 2.006795amostra <- sample(1:length(treatment), size = 1000)
df <- data.frame(y = c(y_1, y_0)[amostra], x=c(x, x)[amostra], treatment = treatment[amostra])
reg <- lm(y ~ 1, data=df)
summary(reg)##
## Call:
## lm(formula = y ~ 1, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -7.2271 -1.6225 0.0041 1.6811 8.4275
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.99604 0.07751 25.75 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.451 on 999 degrees of freedom##
## Call:
## lm(formula = y ~ x, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.6926 -1.0661 -0.0424 1.0582 3.4882
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.00829 0.04511 44.52 <2e-16 ***
## x 1.98185 0.04486 44.18 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.426 on 998 degrees of freedom
## Multiple R-squared: 0.6617, Adjusted R-squared: 0.6613
## F-statistic: 1952 on 1 and 998 DF, p-value: < 2.2e-16## Ignorability apenas com CIA (x)
library(arm)
x <- rnorm(n)
treatment <- ifelse(x > 0, 1,0)
gamma <- 2
tau <- -2 # ATE Average Treatment Effect (ATE) or Average Causal Effect (ACE)
alpha <- 1
nu <- rnorm(n)
eta <- gamma*x + nu
y <- alpha + tau*treatment + eta
df <- data.frame(y=y, x=x, treatment = treatment)
reg3 <- lm(y ~ treatment, data=df)
summary(reg3)##
## Call:
## lm(formula = y ~ treatment, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -6.9323 -1.0549 -0.0142 1.0310 6.5146
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.62909 0.02250 -27.96 <2e-16 ***
## treatment 1.24500 0.03151 39.51 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.575 on 9998 degrees of freedom
## Multiple R-squared: 0.1351, Adjusted R-squared: 0.135
## F-statistic: 1561 on 1 and 9998 DF, p-value: < 2.2e-16##
## Call:
## lm(formula = y ~ treatment + x, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.8184 -0.6634 0.0012 0.6612 3.6943
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.00136 0.01955 51.23 <2e-16 ***
## treatment -1.99905 0.03326 -60.10 <2e-16 ***
## x 2.01035 0.01648 121.98 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.9986 on 9997 degrees of freedom
## Multiple R-squared: 0.6524, Adjusted R-squared: 0.6523
## F-statistic: 9382 on 2 and 9997 DF, p-value: < 2.2e-16library(tidyverse)
library(ggplot2)
df %>%
group_by(treatment) %>%
mutate(uncond_y = mean(y),
erro = (y - uncond_y),
sqs = sum(erro)^2) %>%
ggplot(aes(x, erro )) + geom_point()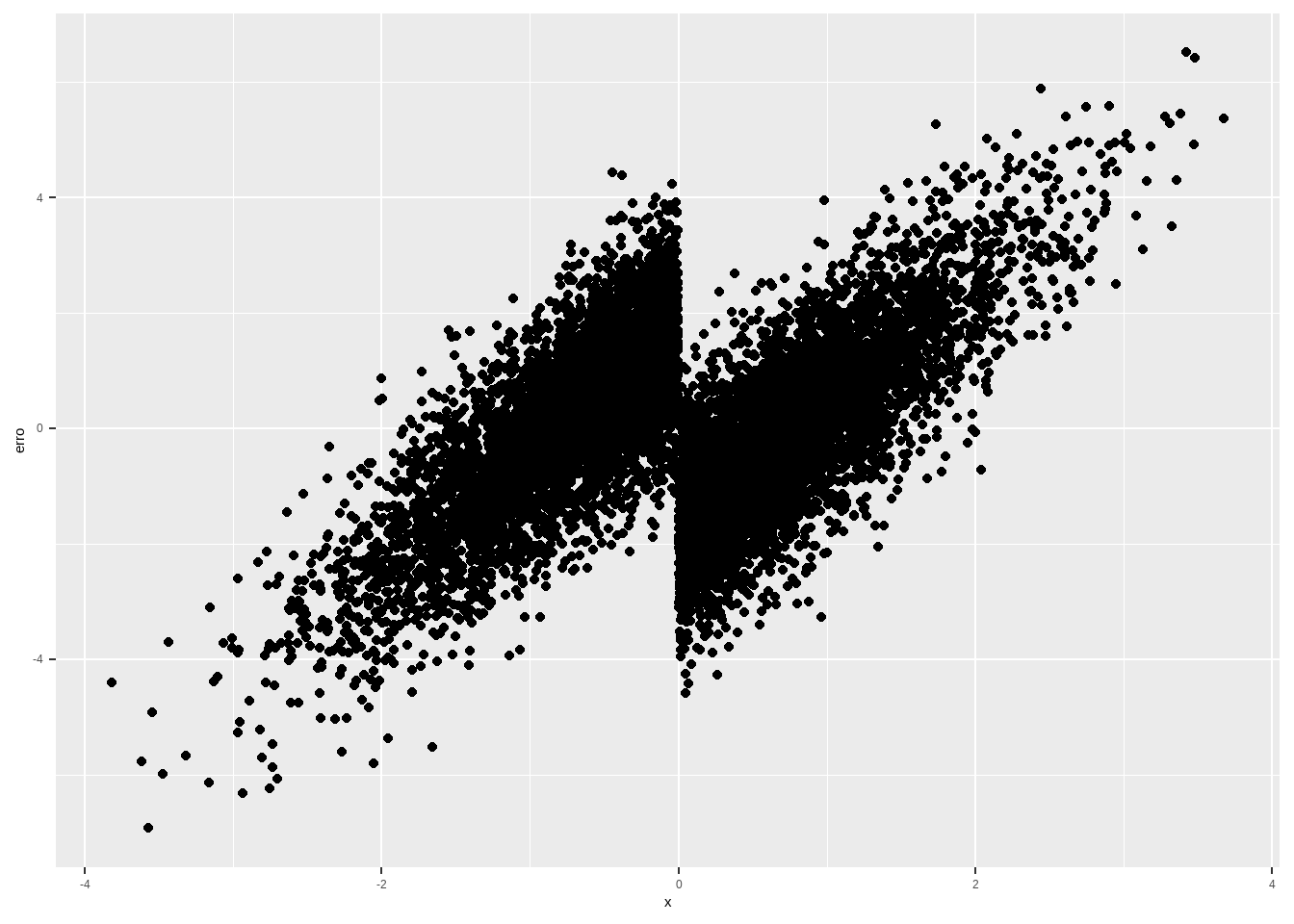
df %>%
mutate(bol_x = ifelse(x > 0 ,1,0)) %>%
group_by(treatment, bol_x) %>%
mutate(cond_y = mean(y)) %>%
ungroup() %>%
mutate(erro = (y - cond_y),
sqs = sum(erro)^2) %>%
ggplot(aes(x, erro )) + geom_point()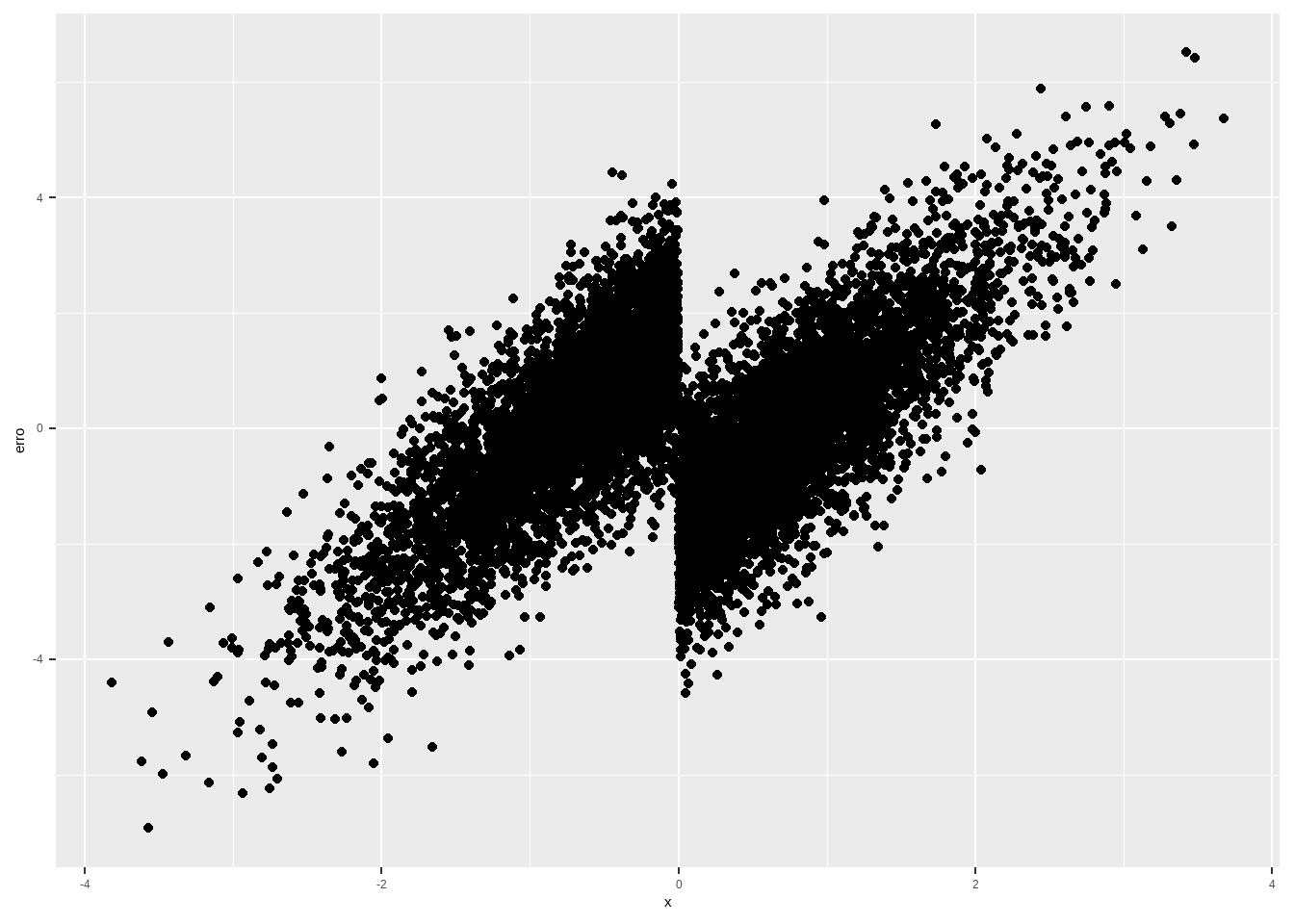
# -5 ocorre 10%,02 10% etc. até 5, 10% das vezes
x <- sample(1:11, size=n, replace=T) - 6
treatment <- ifelse(x > 0, 1,0)
gamma <- 2
tau <- -2 # ATE Average Treatment Effect (ATE) or Average Causal Effect (ACE)
alpha <- 1
nu <- rnorm(n)
eta <- gamma*x + nu
y <- alpha + tau*treatment + eta
df %>%
mutate(bol_x = ifelse(x > 0 ,1,0)) %>%
group_by(treatment, bol_x) %>%
mutate(cond_y = alpha + .5*tau + gamma*x ) %>%
ungroup() %>%
mutate(erro = (y - cond_y),
sqs = sum(erro)^2) %>%
ggplot(aes(x, erro )) + geom_point()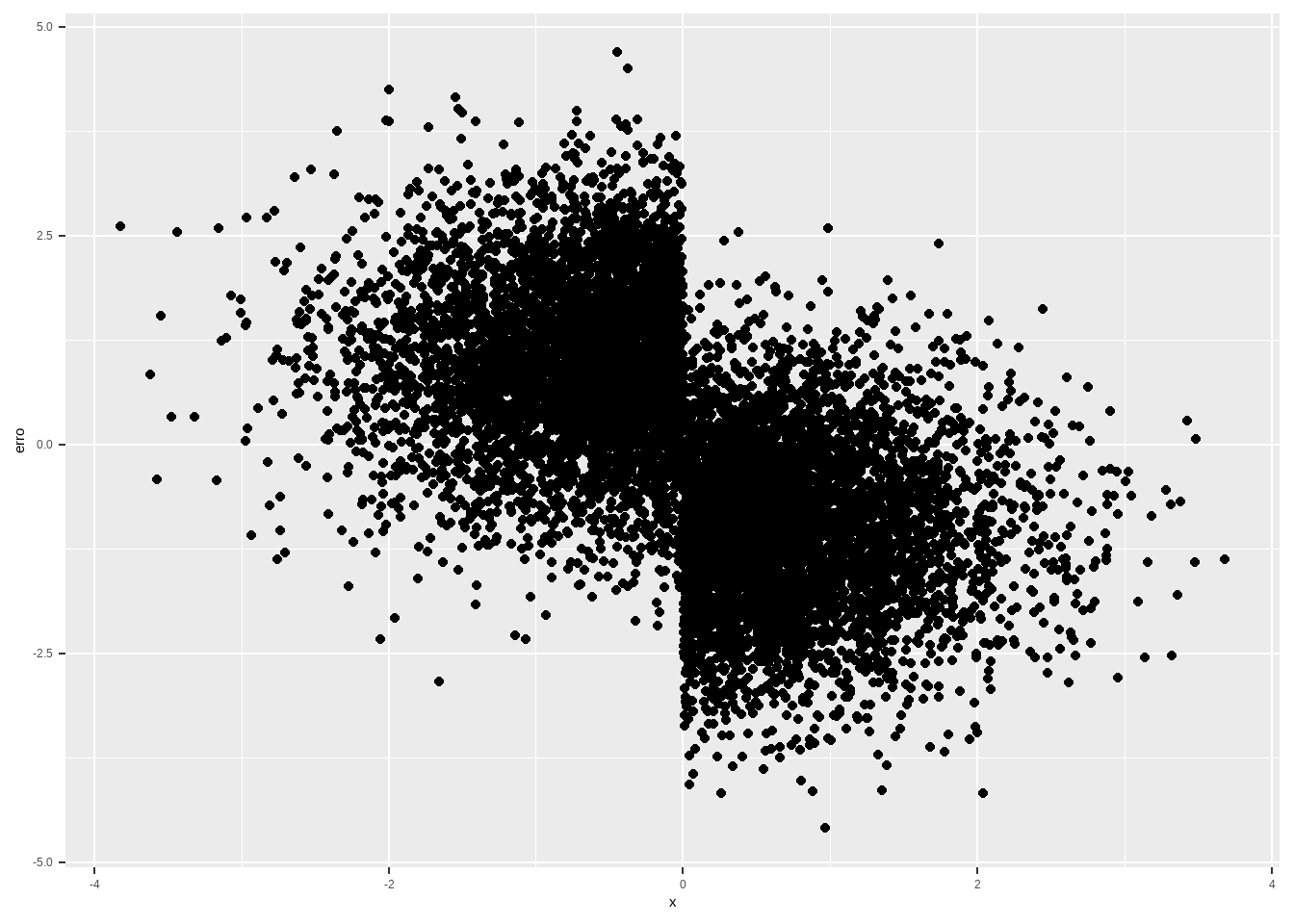
df %>%
mutate(bol_x = ifelse(x > 0 ,1,0),
cond_y = alpha + tau*treatment + gamma*x,
erro = (y - cond_y),
sqs = sum(erro)^2) %>%
ggplot(aes(y=erro, x=x )) + geom_point() + geom_smooth(method="lm")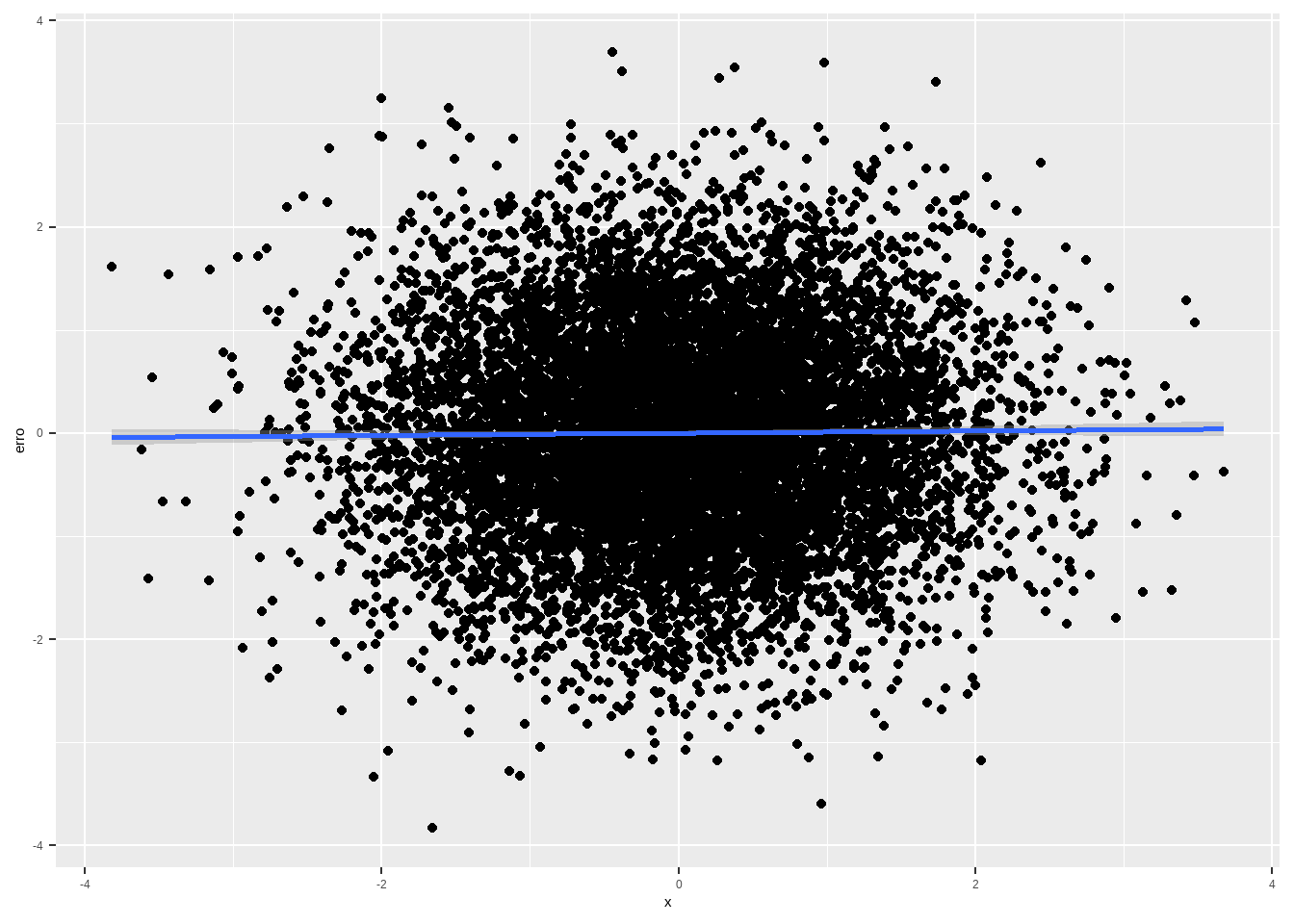
df %>%
mutate(bol_x = ifelse(x > 0 ,1,0),
cond_y = alpha + tau*treatment + gamma*x,
erro = (y - cond_y),
sqs = sum(erro)^2) %>%
summarise(cor(erro, x))## cor(erro, x)
## 1 0.01083649