Capítulo 3 - Revisão de estatística e probabilidade
A média de um conjunto de valores é dada pela soma dos valores, dividido pelo número de observações. Matematicamente: \(media = \sum_{i=1}^n{x_i}/n\) para observações \(\{ x_1, x_2, x_3, ..., x_n \}\)
Em geral, as observações são uma amostra, e falamos de média amostral, \(\overline x\). Ou seja:
\(\overline x = \sum_{i=1}^n{x_i}/n\)
Exercício 1. Vamos calcular, no R, a média das seguintes amostras:
\(\{1,2,3,4,5,6,7,8,9,10\}\)
\(\{5,5,5,5,5,5,5\}\)
\(\{1,3,5,7,9,11\}\)
\(\{-5,-4,-3,-2,-1,1,2,3,4,5\}\)
Código no R
## [1] 5.5## [1] 5## [1] 6## [1] 0## [1] 03.1 Variável Aleatória
Uma variável aleatória (v.a.) mede numericamente resultados de eventos aleatórios. Por exemplo, um dado de \(6\) faces possui um espaço amostral de eventos possíveis dados pelos números \(\{1,2,3,4,5,6\}\). Ao atribuirmos uma probabilidade a cada resultado possível do espaço amostral, por exemplo \(1/6\), temos uma distribuição de probabilidade.
Variáveis aleatórias podem ser discretas ou contínuas. Uma v.a. discreta pode assumir um número finito (contável) de valores. Já uma contínua pode assumir infinitos (não-contáveis) valores.
Um conjunto é contável se ele for finito ou se puder ser estabelecida uma correspondência um para um com o conjunto (infinito) dos números naturais.
3.2 Esperança matemática
A esperança de uma variável aleatória discreta \(X\), cuja probabilidade de massa de \(x \in X\) é dada por \(p(x)\), é definida por: \(\sum(x*p(x))\).
A esperança de uma v.a. contínua X, cuja densidade é \(f(x)\), é definida por: \(\int f(x)*x\,dx\).
Similarmente, para a mesma v.a. X acima, a esperança de uma função \(h(X)\) é dada por \(\int f(x)*h(x)\,dx\) e analogamente para o caso discreto.
3.3 Variância
A variância de uma variável aleatória \(X\) é dada por:
Definição 1. \(Var(X) = \mathbb{E}[(X - \mathbb{E}[X])^2]\).
A Covariância de duas v.a. \(X\) e \(Y\) é definida como: \(Cov(X,Y) = \mathbb{E}[(X - \mathbb{E}[X])*(Y - \mathbb{E}[Y])]\).
Notem que \(Cov(X,X) = Var(X)\).
A covariância é positiva quando ambos X e Y tendem a ter valores acima (ou abaixo) de sua média simultaneamente, enquanto ela é negativa quando uma v.a. tende a ter valores acima da sua média e a outra abaixo.
3.4 Álgebra com Esperança, Variância e Covariância
Sejam \(a\) e \(b\) constantes.
- Linearidade da Esperança \(\mathbb{E}[aX + bY] =\mathbb{E}[aX] + \mathbb{E}[by] = a*\mathbb{E}[X] + b*\mathbb{E}[Y]\)
Exercício: verifique, com exemplos, que isso é verdade.
- Identidade da variância
\(Var(X) = \mathbb{E}[(X - \mathbb{E}[X])^2] = \mathbb{E}[X^2] - \mathbb{E}^2[X]\)
A prova será demonstrada mais adiante.
- Identidade da Covariância
\(Cov(X,Y) = \mathbb{E}[X*Y] - \mathbb{E}[X]*\mathbb{E}[Y] = \mathbb{E}[(X - \mathbb{E}[X])*(Y - \mathbb{E}[Y])]\)
Exercício para o leitor. Prove que isso é verdade.
4, Covariância é simétrica
\(Cov(X,Y) = Cov(Y,X)\)
Variância não é linear \(Var(a*X + b) = a^2*Var(x)\)
Covariância não é linear
\(Cov(a*X + b,Y) = a*Cov(Y,X)\)
3.5 Prova da identidade da variância
Vamos mostrar que \(\mathbb{E}[(X - \mathbb{E}[X])^2] = \mathbb{E}[X^2] - \mathbb{E}^2[X]\)
Começamos expandido o quadrado da esperança: \(Var(X) = \mathbb{E}[(X - \mathbb{E}[X])^2] = \mathbb{E}[(X - \mathbb{E}[X]) * (X - \mathbb{E}[X])]\).
Aplicando a regra do quadrado, temos: \(\mathbb{E}[(X - \mathbb{E}[X]) * (X - \mathbb{E}[X])] = \mathbb{E}[(X^2 - 2* \mathbb{E}[X]*X + \mathbb{E}[X]^2)]\)
Pela propriedade da experança, sabemos que, sejam \(A\) e \(B\) duas v.a. independentes, então \(\mathbb{E}[A + B] = \mathbb{E}[A] + \mathbb{E}[B]\). Então:
\(Var(X) = \mathbb{E}[X^2] - \mathbb{E}[2*\mathbb{E}[X]*X] + \mathbb{E}[\mathbb{E}[X]^2]]\)
- Outra propriedade da esperança é que, seja \(a\) uma constante e \(X\) uma v.a., então \(\mathbb{E}[a*X] = a*\mathbb{E}[X]\).
\(Var(X) = \mathbb{E}[X^2] - 2*\mathbb{E}[\mathbb{E}[X]*X] + \mathbb{E}[\mathbb{E}[X]^2]]\)
- Nós sabemos que \(\mathbb{E}[X]\) é uma constante (é uma média da v.a.). E a média de uma constante é a própria constante. Portanto, \(\mathbb{E}[\mathbb{E}[X]] = \mathbb{E}[X]\). E usaremos também que \(\mathbb{E}[a*X] = a*\mathbb{E}[X]\) e, por fim, o fato de que uma constante ao quadrado é em si uma constante.
\(Var(X) = \mathbb{E}[X^2] - 2*\mathbb{E}[X] * \mathbb{E}[\mathbb{E}[X]] + \mathbb{E}[X]^2\)
\(Var(X) = \mathbb{E}[X^2] - 2*\mathbb{E}[X] * \mathbb{E}[X] + \mathbb{E}[X]^2\)
\(Var(X) = \mathbb{E}[X^2] - 2*\mathbb{E}[X]^2 + \mathbb{E}[X]^2\)
\(Var(X) = \mathbb{E}[X^2] - \mathbb{E}[X]^2\)
Como Queriamos Demonstrar (CQD).
3.6 Distribuição de Probabilidade Conjunta
A Distribuição de probabilidade conjunta de \(X\) e \(Y\) (definida no mesmo espaço de probabilidade) é uma distribuição de probabilidade dos pares \((x,y)\) e descreve como os valores de \(X\) e \(Y\) variam conjuntamente. Cada uma das distribuições \(X\) e \(Y\) sozinhas são chamadas de distribuições marginais. Uma distribuição conjunta é como uma máquina que, de acordo com certas regras de probabilidade, retorna dois pares de valores.
ex. 1. Roleta. Em um casino, um jogo comum é a roleta. Ela consiste normalmente de 32 números (0 a 31), e cada número tem uma cor (preto, vermelho ou verde). Ao girar a roleta, ela solta um número e uma cor. Portanto, podemos pensar que a roleta é uma distribuição conjunta de duas variáveis (números e cores).
Ex. 2.: Considere um dado de 4 faces \(( 1, 2, 3, 4 )\). Seja \(X\) a soma dos números dos dois dados, e \(Y\) o maior valor dos dois dados. O espaço amostral é dado pela tabela abaixo.
library(knitr)
library(dplyr)
library(kableExtra)
#Definir o espaço amostral
espaco_amostral <- expand.grid(1:4, 1:4)
espaco_amostral$X <- espaco_amostral$Var1 + espaco_amostral$Var2
espaco_amostral$Y <- pmax(espaco_amostral$Var1, espaco_amostral$Var2)
# Criar a tabela
kable(espaco_amostral, col.names = c("resultado do primeiro dado", "resultado do segundo dado", "X", "Y"),
caption = "Tabela representando a soma (X) and o maior valor (Y) do lançamento de dois dados de quatro lados") %>%
kable_styling(bootstrap_options = "striped")## Warning in attr(x, "align"): 'xfun::attr()' is deprecated.
## Use 'xfun::attr2()' instead.
## See help("Deprecated")
## Warning in attr(x, "align"): 'xfun::attr()' is deprecated.
## Use 'xfun::attr2()' instead.
## See help("Deprecated")| resultado do primeiro dado | resultado do segundo dado | X | Y |
|---|---|---|---|
| 1 | 1 | 2 | 1 |
| 2 | 1 | 3 | 2 |
| 3 | 1 | 4 | 3 |
| 4 | 1 | 5 | 4 |
| 1 | 2 | 3 | 2 |
| 2 | 2 | 4 | 2 |
| 3 | 2 | 5 | 3 |
| 4 | 2 | 6 | 4 |
| 1 | 3 | 4 | 3 |
| 2 | 3 | 5 | 3 |
| 3 | 3 | 6 | 3 |
| 4 | 3 | 7 | 4 |
| 1 | 4 | 5 | 4 |
| 2 | 4 | 6 | 4 |
| 3 | 4 | 7 | 4 |
| 4 | 4 | 8 | 4 |
Se supusermos que todos os números possuem a mesma chance de sair quando jogamos os dados, então, a distribuição conjunta de \(X\) e \(Y\) pode ser dada por:
# Definir os valores de (x, y) e P(X = x, Y = y)
valores <- c("(2, 1)", "(3, 2)", "(4, 2)", "(4, 3)", "(5, 3)", "(5, 4)", "(6, 3)", "(6, 4)", "(7, 4)", "(8, 4)")
probabilidades <- c(0.0625, 0.1250, 0.0625, 0.1250, 0.1250, 0.1250, 0.0625, 0.1250, 0.1250, 0.0625)
# Criar a tabela
tabela <- data.frame("(x, y)" = valores, "P(X = x, Y = y)" = probabilidades)
# Formatar a tabela
kable(tabela, caption = "Tabela representando a distribuição conjunta da soma (X) e o maior (Y) de dois lançamentos de um dado de quatro faces",
col.names = c("$(X,Y)$", "$P(X=x, Y=y)$")) %>%
kable_styling(bootstrap_options = "striped")## Warning in attr(x, "align"): 'xfun::attr()' is deprecated.
## Use 'xfun::attr2()' instead.
## See help("Deprecated")
## Warning in attr(x, "align"): 'xfun::attr()' is deprecated.
## Use 'xfun::attr2()' instead.
## See help("Deprecated")| \((X,Y)\) | \(P(X=x, Y=y)\) |
|---|---|
| (2, 1) | 0.0625 |
| (3, 2) | 0.1250 |
| (4, 2) | 0.0625 |
| (4, 3) | 0.1250 |
| (5, 3) | 0.1250 |
| (5, 4) | 0.1250 |
| (6, 3) | 0.0625 |
| (6, 4) | 0.1250 |
| (7, 4) | 0.1250 |
| (8, 4) | 0.0625 |
3.7 Probabilidade Condicional
Nós vimos o que é uma distribuição de probabilidade conjunta. É comum que nós tenhamos apenas uma observação parcial sobre uma das variáveis. Digamos, que \(y = 2\). De posse dessa informação, como podemos atualizar nossa tabela de probabilidades? Se o maior valor foi \(2\), então a soma dos dados \(X\) só pode ser 3 ou 4. Se a soma for 3, temos algo como \((1,2)\) ou \((2,1)\). Se a soma for 4, então deve ter saído \((2,2)\). Esse é o novo espaço amostral dado que \(y=2\).Todos os outros números não podem ocorrer e, portanto, possuem probabilidade zero. Logo, \(P(X=1|Y=2) = 2/3\) e \(P(X=2|Y=2) = 1/3\).
Isso é o que chamamos de probabilidade condicional. No caso, a probabilidade condicional de \(X\), dado \(Y=y\).
A probabilidade condicional é em si uma distribuição de probabilidade. Do mesmo jeito que temos as distribuições de probabilidade de \(X\), de \(Y\) e de \(X,Y\), também temos a de \(X|y=y\) (e, claro, a de \(Y|X=x\)). A tabela abaixo apresenta essa distribuição de probabilidade condicional para o caso de \(Y=2\).
# Definir os valores de (x, y) e P(X = x, Y = y)
valores <- c("(2, 1)", "(3, 2)", "(4, 2)", "(4, 3)", "(5, 3)", "(5, 4)", "(6, 3)", "(6, 4)", "(7, 4)", "(8, 4)")
probabilidades <- c(0, 2/3, 1/3, 0, 0, 0, 0, 0, 0, 0)
# Criar a tabela
tabela <- data.frame("(x, y)" = valores, "P(X = x| Y = 2)" = probabilidades)
# Formatar a tabela
kable(tabela, caption = "Tabela representando a distribuição conjunta da soma (X) e o maior (Y) de dois lançamentos de um dado de quatro faces",
col.names = c("$(X,Y)$", "$P(X=x| Y=2)$")) %>%
kable_styling(bootstrap_options = "striped")## Warning in attr(x, "align"): 'xfun::attr()' is deprecated.
## Use 'xfun::attr2()' instead.
## See help("Deprecated")
## Warning in attr(x, "align"): 'xfun::attr()' is deprecated.
## Use 'xfun::attr2()' instead.
## See help("Deprecated")| \((X,Y)\) | \(P(X=x&#124; Y=2)\) |
|---|---|
| (2, 1) | 0.0000000 |
| (3, 2) | 0.6666667 |
| (4, 2) | 0.3333333 |
| (4, 3) | 0.0000000 |
| (5, 3) | 0.0000000 |
| (5, 4) | 0.0000000 |
| (6, 3) | 0.0000000 |
| (6, 4) | 0.0000000 |
| (7, 4) | 0.0000000 |
| (8, 4) | 0.0000000 |
3.8 Esperança Condicional
Se a probabilidade condicional é uma distribuição de probabilidade no seu próprio direito, então podemos calcular a esperança dessa distribuição, exatamente como fazíamos antes. No caso, falamos de esperança condicional. Qual o valor médio de \(X\), quando \(Y=2\)?
\(3*(2/3) + 4*(1/3)\) \(2 + 4/3 = 6/3 + 4/3 = 10/3 = 3.333\)
A notação matemática para a esperança condicional, nesse caso, é: \(E[X|Y=2]\).
3.9 Projeção Linear
A projeção linear é uma das formas de interpretar o que a regressão linear está fazendo. Então, vamos entender o que é a projeção linear e como ela se conectar com regressão. Antes disso, vamos garantir que temos uma intepretação geométrica da soma e subtração de vetores, para dpois entender a projeção linear.
3.9.1 Adição de vetores
Considere os vetores \(\vec{u} = (2,1)\) e \(\vec{v} = (1,2)\). Sabemos algebricamente que a soma de \(\vec{u} + \vec{v} = (2+1, 1+2) = (3,3)\). Vejamos isso graficamente.
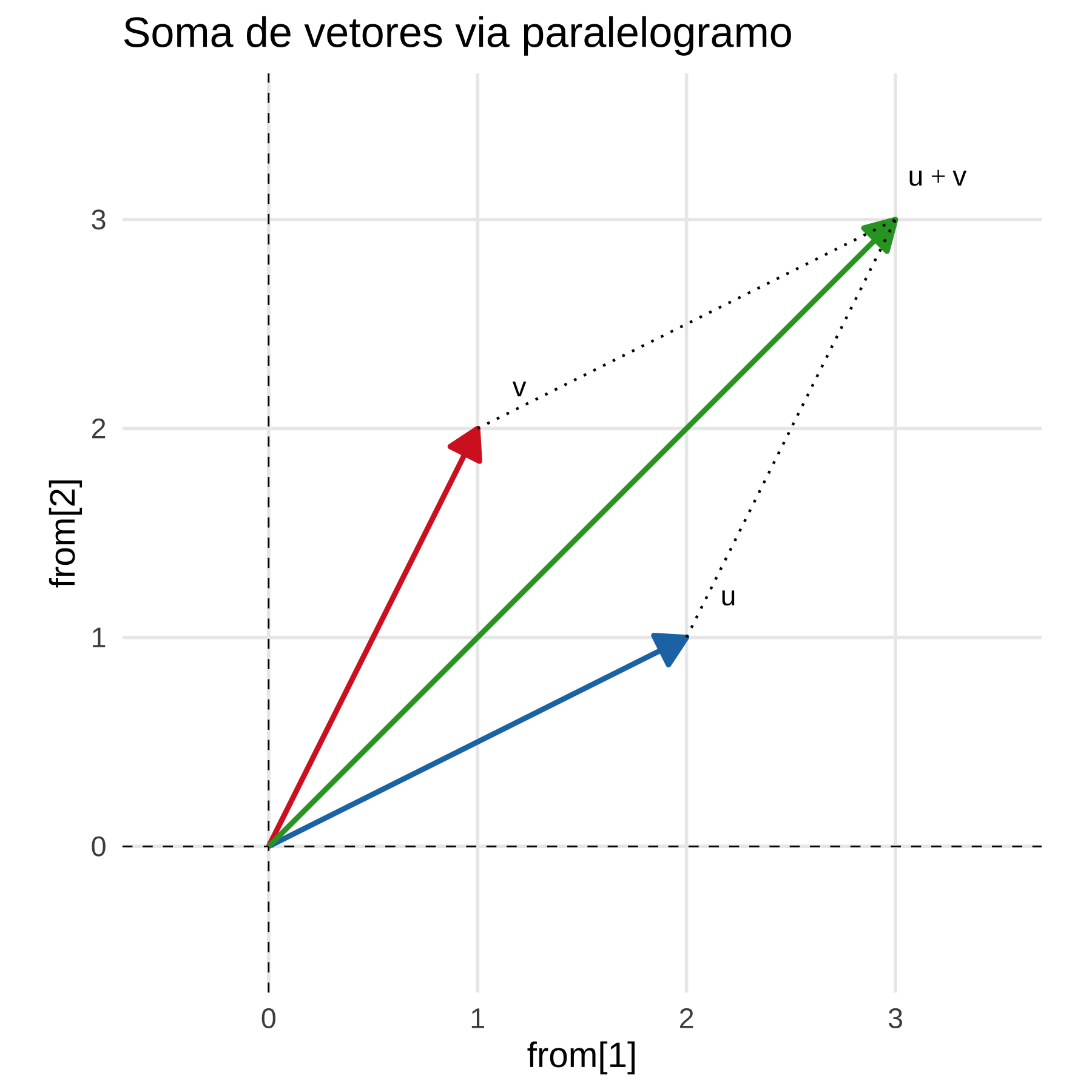
Agora, passemos à subtração. Primeiro, veja que \(-\vec{v}\) é o vetor \(\vec{v}\) em que mudamos o sentido. Algebricamente, sabemos que \(\vec{u} + \vec{v} = (2-1, 1-2) = (1,-1)\). Graficamente, fica como abaixo.
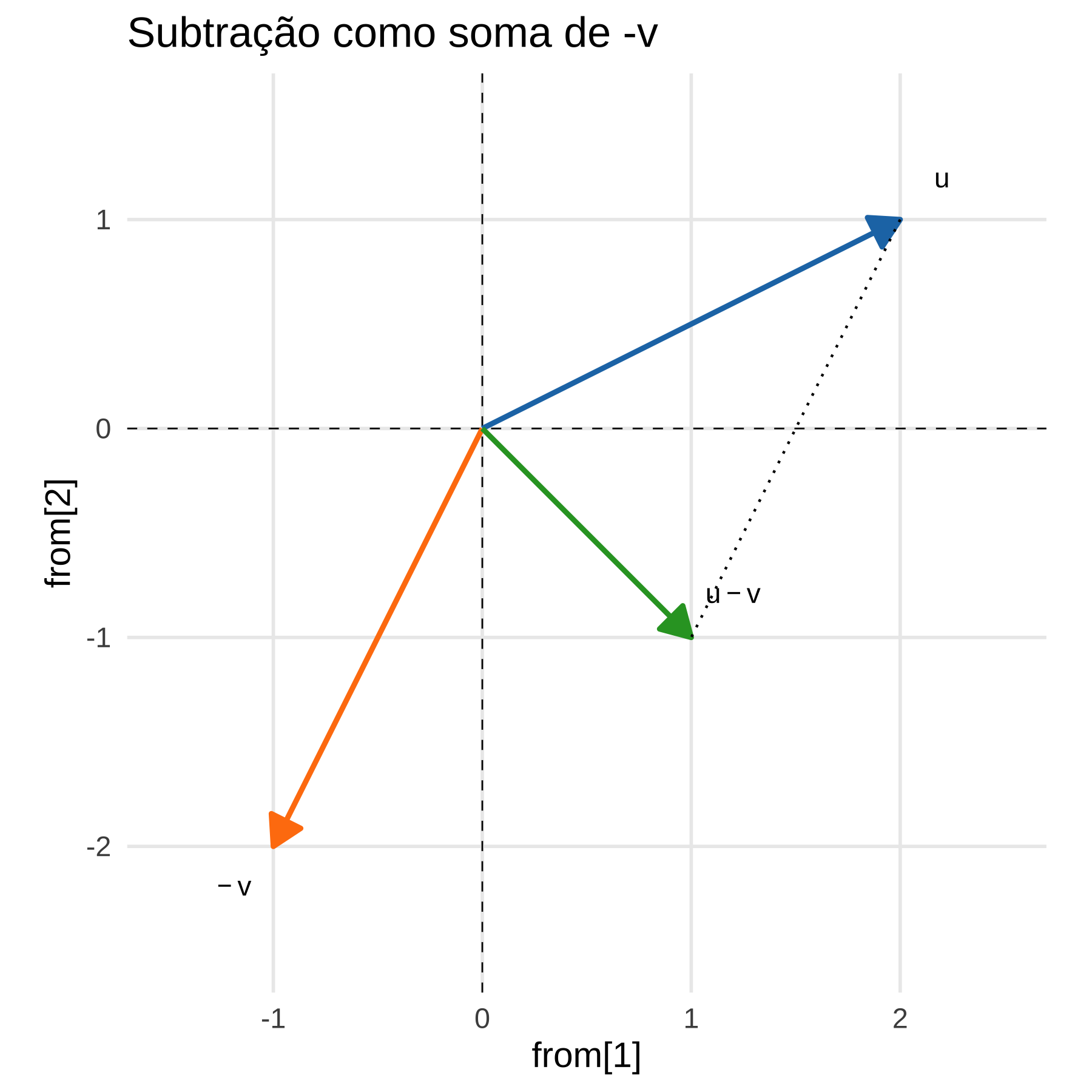
3.9.2 Projeção linear
y <- c(2, 2.5)
# projeção de y em u
proj_coeff <- sum(y * u) / sum(u * u)
proj_y_on_u <- proj_coeff * u
r <- y - proj_y_on_u
# vetores unitários para marcar ângulo reto
u_hat <- u / sqrt(sum(u^2))
n_hat <- c(-u_hat[2], u_hat[1]) # perpendicular a u_hat (rotação 90°)
# cantoneira (marcador de ângulo reto) no ponto da projeção
A <- proj_y_on_u
eps <- 0.25
B <- A + eps * u_hat
C <- A + eps * n_hat
p3 <- base_plot(list(u, y, proj_y_on_u)) +
seg(u, col = "gray40") +
seg(y, col = "#1f77b4") +
seg(proj_y_on_u, col = "#2ca02c") +
# resíduo r: da projeção até y
geom_segment(aes(x = proj_y_on_u[1], y = proj_y_on_u[2],
xend = y[1], yend = y[2]),
arrow = arrow_style, linewidth = 1, color = "#d62728") +
# marcador de ângulo reto em proj_u(y)
geom_segment(aes(x = A[1], y = A[2], xend = B[1], yend = B[2])) +
geom_segment(aes(x = A[1], y = A[2], xend = C[1], yend = C[2])) +
annotate("text", x = y[1] + 0.2, y = y[2], label = "y") +
annotate("text", x = u[1] + 0.2, y = u[2], label = "u") +
annotate("text", x = proj_y_on_u[1] + 0.2, y = proj_y_on_u[2], label = TeX("$\\proj_u (y)$")) +
annotate("text",
x = (y[1] + proj_y_on_u[1]) / 2,
y = (y[2] + proj_y_on_u[2]) / 2 + 0.25,
label = TeX("$r\\,=\\,y- \\proj_u (y)\\;\\perp\\;u$")) +
labs(title = "Projeção de y em u e resíduo perpendicular")
p3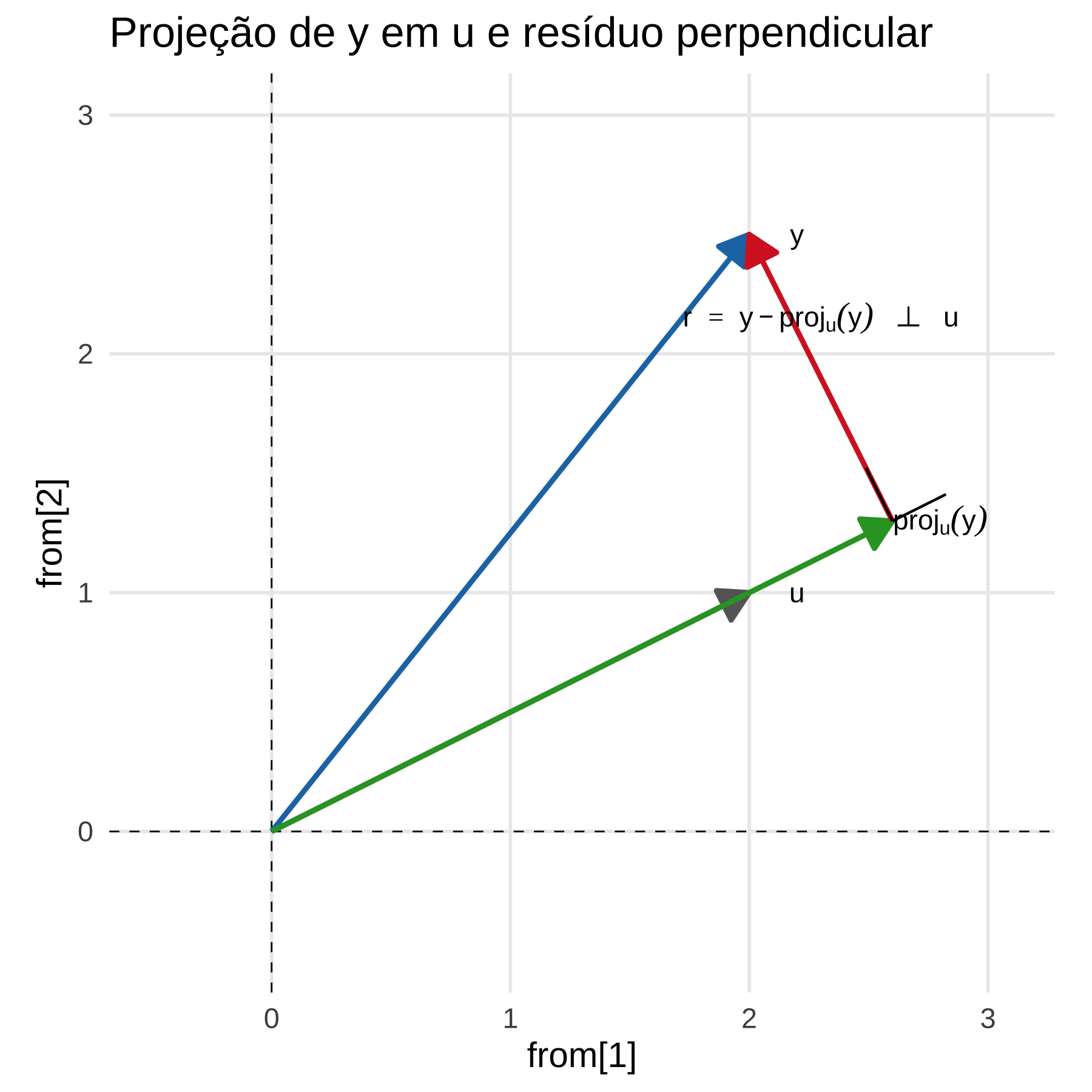
A fórmula da projeção é: \(proj_u (y) = \frac{y \cdot u}{u \cdot u} u\).