Capítulo 14 - Apêndice
Iremos tratar aqui de tópicos especiais. Em primeiro lugar, do R. Vamos listar aqui os pacotes do R que eu mais utilizo e as principais funções.
14.1 Importação
Para ler arquivos em csv ou formato tabular, prefiro a função fread do data.table.
Para ler arquivos de outrossoftwares, como stata ou SPSS, vejam as funções do pacote haven.
Para arquivos em formato xls ou xlsx, do Excel, uso a função read_excel do pacote readxl.
14.2 Gráficos e Tabelas
Para visualização, uso o ggplot e pacotes que dialogam com o ggplot2. A única exceção é para plotar o gráfico da logística, que usei o R base e a função curve.
Para gerar tabelas em Rmarkdown, uso quatro funções (deveria ser mais consistente e usar só uma ou duas), kable do knitr, gt do pacote de mesmo nome, stargazer, também do pacote de mesmo nome e a função etable do pacote fixest, quando rodo regressões desse pacote.
14.3 Limpeza de dados
Para limpeza de dados, além do tidyverse e tidyr, uso o pacote janitor (particularmente a função clean_names) e o pacote lubridate para trabalhar com datas. Com relação a textos, o pacote stringr.
14.4 Modelagem de dados
Para regressões limpes, uso o R base e suas funções lm e glm. Para dados em painel, prefiro o pacote fixest e suas funções, como a feols, que evita de eu ter de chamar o pacote sandwich para erro padrão robusto. O fixest é melhor que o mais tradicional e antigo pacote plm, que era mais usado para dados em painel antigamente. Para modelos Bayesianos, vario entre rstanarm e brms.
14.5 Outros
Checagem do modelo, o pacote performance.
Para testes informais de permutação, o pacote nullabor.
Para instalação de pacotes direto do gihutb, devtools.
Para ajudar na reproducibilidade, uso o pacote here para não vincular aos meus diretórios específicos e evito usar osetwd para apontar o diretório.
14.6 Álgebra Linear
Aqui apresentamos alguns tópicos de álgebra linear que podem ser úteis.
14.6.1 Espaço de vetores e subspaço
O espaço vetorial de dimensão \(n\) é o conjunto infinito de todos os vetores \(x = [x_1, x_2, \cdots, x_n]\), e as coordenadas \(x-i\) podem ser quaisquer números reais.
Dizemos que um subespaço do espaço vetorial \(n\)-dimensional que é gerado por um conjunto de \(k\) vetores \(x = [x_1, x_2, \cdots, x_k]\), em que \(k\) pode ser eventualmente igual a \(n\) (ou menor), é o subconjunto de vetores \(y\) naquele espaço que pode ser expresso como uma combinação linear do conjunto gerador:
\(y = a_1x_1 + a_2x_2 + \cdots + a_kx_k\)
Dizemos que o conjunto de vetores \(x = [x_1, x_2, \cdots, x_k]\) gera o subespaço que ele define.
14.6.2 Projeção linear
# Load necessary library
library(ggplot2)
# Define vectors u and v
u <- c(3, 2)
v <- c(4, 0)
# Calculate the projection of u onto v
proj_v_u <- (sum(u * v) / sum(v * v)) * v
# Create a data frame for plotting
data <- data.frame(
x = c(0, u[1], 0, v[1], 0, proj_v_u[1]),
y = c(0, u[2], 0, v[2], 0, proj_v_u[2]),
label = c("Origin", "u", "Origin", "v", "Origin", "Projection")
)
# Create the plot
ggplot(data) +
geom_segment(aes(x = x[1], y = y[1], xend = x[2], yend = y[2]), arrow = arrow(length = unit(0.3, "cm")), color = "blue", size = 1.2) +
geom_segment(aes(x = x[3], y = y[3], xend = x[4], yend = y[4]), arrow = arrow(length = unit(0.3, "cm")), color = "red", size = 1.2) +
geom_segment(aes(x = x[5], y = y[5], xend = x[6], yend = y[6]), linetype = "dashed", color = "green", size = 1.2) +
annotate("text", x = u[1] + 0.5, y = u[2], label = "u", color = "blue") +
annotate("text", x = v[1] + 0.5, y = v[2], label = "v", color = "red") +
annotate("text", x = proj_v_u[1] + 0.5, y = proj_v_u[2], label = "proj_v_u", color = "green") +
xlim(0, max(u[1], v[1], proj_v_u[1]) + 1) +
ylim(0, max(u[2], v[2], proj_v_u[2]) + 1) +
theme_minimal() +
labs(title = "Projection of Vector u onto Vector v",
x = "X-axis",
y = "Y-axis")## Warning in geom_segment(aes(x = x[1], y = y[1], xend = x[2], yend = y[2]), : All aesthetics have length 1, but the data has 6 rows.
## ℹ Please consider using `annotate()` or provide this layer with data
## containing a single row.## Warning in geom_segment(aes(x = x[3], y = y[3], xend = x[4], yend = y[4]), : All aesthetics have length 1, but the data has 6 rows.
## ℹ Please consider using `annotate()` or provide this layer with data
## containing a single row.## Warning in geom_segment(aes(x = x[5], y = y[5], xend = x[6], yend = y[6]), : All aesthetics have length 1, but the data has 6 rows.
## ℹ Please consider using `annotate()` or provide this layer with data
## containing a single row.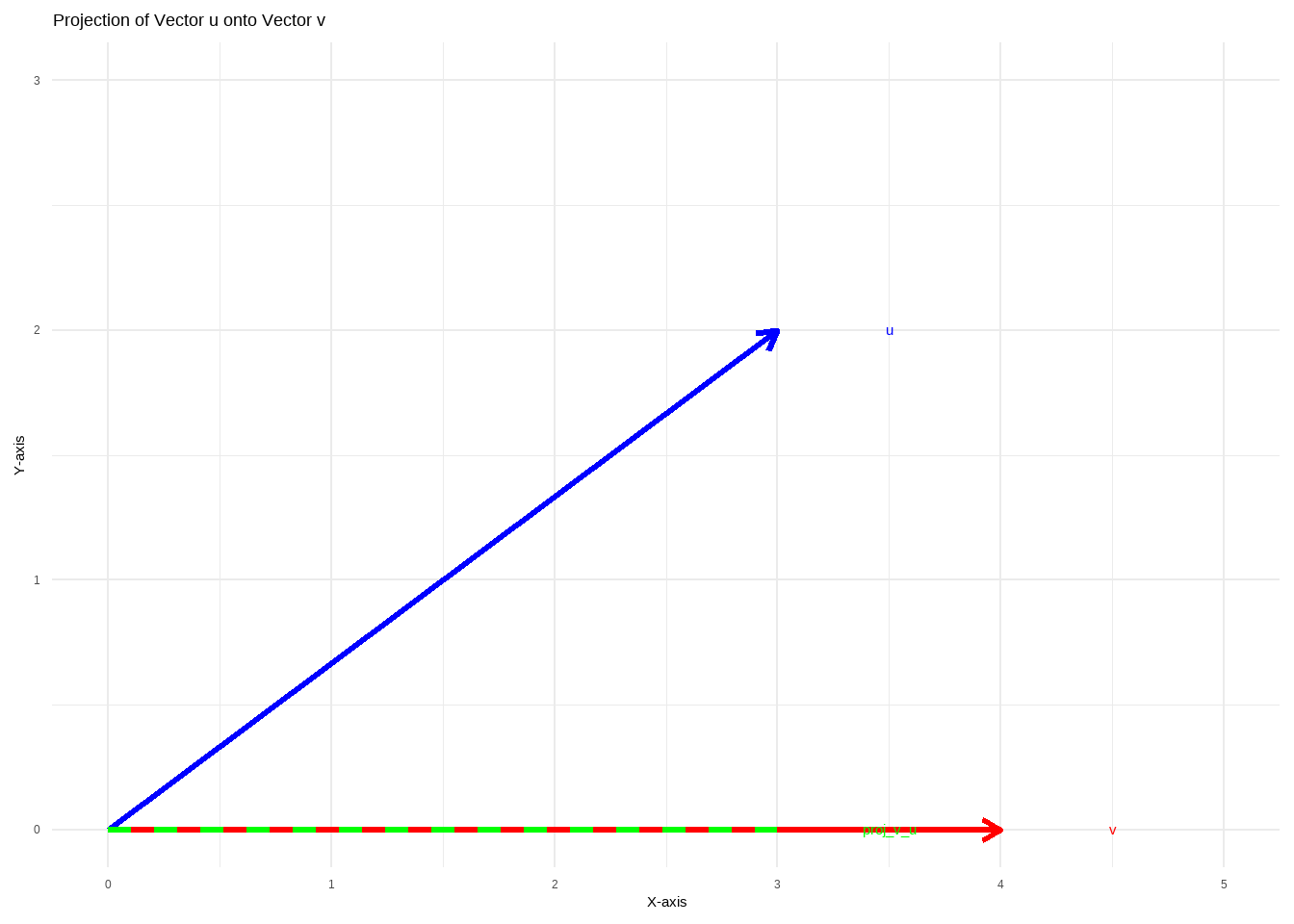
The plot above shows the vectors \(\mathbf{u}\) (in blue) and \(\mathbf{v}\) (in red), along with the projection of \(\mathbf{u}\) onto \(\mathbf{v}\) (in green, dashed line). The projection is the closest point on the line defined by \(\mathbf{v}\) to the point represented by \(\mathbf{u}\). This visualization helps in understanding how projections work in a geometric sense.
14.7 Dados Espaciais
Há dois tipos de dados espaciais diferentes que se traduzem em visualizações distintas. Em primeiro lugar, temos dados espaciais em pontos, que podem ser plotados como conjuntos de pontos em um mapa. Designam localizações específicas, como cidades ou quaisquer objetos discretos definidos em um espaço. E em segundo lugar, temos dados espaciais de polígonos, que representam uma sequência de pontos conectados espacialmente (em geral fronteiras) que formam um área.