Capítulo 13 - GLM
GLM é a sigla de Modelos Lineares Generalizados. A regressão logística pode ser considerada como um dos tipos de modelos lineares generalizados. Vamos nos concentrar em entender a regressão logística, como ela se conecta com GLM e, rapidamente, ver outros modelos de GLM que existem, como Poisson e probit. Até o momento, variáveis resposta binárias foram modeladas com regressão linear.
13.1 PLM
Até o momento, variáveis respostas binárias foram modeladas com regressão linear.
\[ y_i \sim N(\alpha + \beta x_i, \sigma^2) \]
Nessa parametrização do modelo de regressão, vemos que a resposta é modelada como uma variável Gaussiana e, portanto, é uma variável contínua (em vez de binária). Além disso, não está limitada, possuindo suporte entre −∞ e +∞. Esses modelos são chamados também de Modelos de Probabilidade Linear (MPL, ou LPM na sigla em inglês). Explicaremos mais à frente porque são chamados desse modo, após apresentarmos a regressão logística e probit. E então poderemos comparar modelos logísticos ou probit e MPL.
13.2 Logística
Há várias formas de apresentar e/ou justificar a regressão logística. Qual delas você irá usar para pensar esse tipo de modelo depende do seu problema de pesquisa e das suas preferências sobre o que funciona melhor para você.
13.2.1 Logística como melhoria em relação ao MPL
Como vimos, o problema da regressão linear para dados binários é que considera que a variável resposta possui distribuição Gaussiana. Faz muito mais sentido modelar dados binários como seguindo uma distribuição de Bernoulli, com parâmetro \(p_i\). Poderíamos, portanto, tentar reescrever um modelo para \(y\) binário da seguinte forma:
\[ y_i \sim Ber(p_i) \] Em que \(p_i\) é a probabilidade de sucesso para a unidade \(i\). Dessa forma, contudo, não incluí nenhum preditor para estimar o \(p_i\), e gostaríamos de fazê-lo. Posso então escrever algo como: \[ p_i(x_i) = \alpha + \beta x_i \]
O problema dessa formulação é que probabilidades devem estar entre 0 e 1, e nada garante que \(\alpha + \beta x_i\) seja um número entre 0 e 1. Então, uma saída é tentar achar uma função \(f\) que transforme \(\alpha + \beta x_i\) em números entre 0 e 1, ou seja, \(0 \le f(\alpha + \beta x_i) \le 1\). E uma função que tem essa propriedade é a logística padrão (também chamada de sigmoide), dada por:
\[ f(x) = \frac{1}{1 + \exp(-x)} \]
Então, nossa relação entre a probabilidade e os preditores fica:
\[ p_i = \frac{1}{1 + \exp(-(\alpha + \beta x_i))} \]
Conectando com nossa variável resposta, temos:
\[ y_i \sim Ber(\frac{1}{1 + \exp(-(\alpha + \beta x_i))}) \] A probabilidade de sucesso, condicional ao preditor, fica então: \[\begin{align} Pr(y_i=1|x) = \frac{1}{1 + \exp(-(\alpha + \beta x_i))} \tag{13.1} \end{align}\]
Assim, a modelagem de variável binária por meio da regressão linear pode ser pensada como um modelo em que a probabilidade \(p_i\) é modelada sem a função logística, o que significa que podemos acabar com previsões de probabilidades negativas ou maiores que 1, o que não faz sentido. Essa é uma razão para usar modelos logísticos em vez de lineares.
13.2.2 Logito
Às vezes a logística é designada como a função inversa da logito, em que a logito é dada por: \[ logito(p) = log(\frac{p}{1-p}) \] Para entender isso, vamos lembrar que, se \(f(x) = x + 2\) é uma função, sua inversa \(f^{-1}(x)\), se existir, pode ser descoberta pelo algoritmo em que chamamos \(f(x)\) de \(y\), trocamos \(y\) por \(x\) e resolvemos para \(y\): \[\begin{align} y = x + 2 \\ x = y + 2 \\ y = x - 2 \\ f^{-1}(x) = x - 2 \end{align}\]
Para uma função \(f(x) = log(x+2)\), a inversa é:
\[\begin{align} y = log(x + 2) \\ x = log(y + 2) \\ \exp(x) = \exp(log(y + 2)) \\ \exp(x) = y + 2 \\ y = \exp(x) + 2 \\ f^{-1}(x) = \exp(x) + 2 \end{align}\]
Então, se \(f(X) = log(x)\), \(f^{-1}(x) = \exp(x)\). Disso se segue que:
\[\begin{align} f(x) = log(\frac{x}{1-x}) \\ y = log(\frac{x}{1-x}) \\ x = log(\frac{y}{1-y}) \\ \exp(x) = \exp(log(\frac{y}{1-y})) \\ \exp(x) = \frac{y}{1-y} \\ \exp(x)(1-y) = y \\ \exp(x)- y\exp(x) = y \\ \exp(x) = y + y\exp(x) \\ \exp(x) = y(1 + \exp(x)) \\ \frac{\exp(x)}{(1 + \exp(x))} = y \\ f^{-1}(x) = \frac{\exp(x)}{1 + \exp(x)} \\ f^{-1}(x) = \frac{\frac{\exp(x)}{\exp(x)}}{\frac{1 + \exp(x)}{\exp(x)}} \\ f^{-1}(x) = \frac{1}{\exp(-x) + 1}\\ f^{-1}(x) = \frac{1}{1 + \exp(-x)}\\ \end{align}\]
No R, podemos acessar as duas funções por meio de:
E podemos modelar os dados de uma logística com nosso exemplo do Latinobarômetro usando apenas um preditor, ideologia, para simplificar.
library(here)
library(data.table)
library(tidyverse)
library(sjlabelled) # pra remover labelled variables
library(haven)
library(janitor)
library(lubridate)
library(knitr)
library(broom)
## dados
# https://www.latinobarometro.org/latContents.jsp
lat_bar23 <- sjlabelled::read_spss(here("Dados", "Latinobarometro_2023_Eng_Spss_v1_0.sav"),
drop.labels = TRUE) %>%
mutate(S17 = as.Date(as.character(S17), "%Y%m%d")) %>%
clean_names()## Invalid date string (length=9): 09 032 23# get_label(lat_bar23)
lat_bar23 <- lat_bar23 %>%
mutate(data_base = as.Date(paste(diareal, mesreal, "2023", sep="-"), "%d-%m-%Y"),
idade = year(as.period(interval(s17,data_base))),
econ_12_meses = ifelse(p6stgbs %in% c(1,2), "better",
ifelse(p6stgbs == 8, NA, "other")),
econ_12_meses = relevel(as.factor(econ_12_meses), ref = "other"),
aprovacao_presidente = ifelse(p15stgbs == 0, NA, p15stgbs),
ideologia = ifelse(p16st %in% c(97, 98, 99), NA, p16st),
votaria_governo = ifelse(perpart == 4, NA,
ifelse(perpart == 1, 1, 0)),
genero = factor(sexo, labels = c("homem", "mulher")),
evangelico = ifelse(s1 %in% c(0,98), NA,
ifelse(s1 %in% c(2,3,4,5), 1, 0))) # não considera adventista, testemunha Jeová, Mórmon## Warning: There was 1 warning in `.fun()`.
## ℹ In argument: `idade = year(as.period(interval(s17, data_base)))`.
## Caused by warning in `class(xx) <- cl`:
## ! Definindo class(x) para múltiplas strings ("POSIXct", "POSIXt", ...); resultado não será mais um objeto S4br_latbar_23 <- lat_bar23 %>%
mutate(idenpa = remove_all_labels(idenpa)) %>% # haven_labelled problems
filter(idenpa == 76) %>% ## seelciona brasil
filter(!is.na(votaria_governo) & !is.na(evangelico) & !is.na(ideologia) & !is.na(econ_12_meses))
reg_logistica <- glm(votaria_governo ~ ideologia, data=br_latbar_23,
family=binomial(link= "logit"))
reg_logistica %>%
tidy() %>%
kable()| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 3.1399152 | 0.3377743 | 9.295898 | 0 |
| ideologia | -0.2850991 | 0.0385935 | -7.387224 | 0 |
# plotando # usando base R
# código adaptado de Regression and Other Stories (Gelman et. al.)
library(arm)
n <- nrow(br_latbar_23)
ideologia_jitt <- br_latbar_23$ideologia + runif(n, -.2, .2)
vote_jitt <- br_latbar_23$votaria_governo + ifelse(br_latbar_23$votaria_governo==0, runif(n, .005, .05), runif(n, -.05, -.005))
curve(invlogit(reg_logistica$coef[1] + reg_logistica$coef[2]*x), from = -5,to=24, ylim=c(0,1), xlim=c(-5, 24), xaxt="n", xaxs="i",
ylab="Pr (voto governo)", xlab="Ideologia", lwd=.5, yaxs="i")
curve(invlogit(reg_logistica$coef[1] + reg_logistica$coef[2]*x), 1, 11, lwd=3, add=TRUE)
axis(1, 1:11)
mtext("(left)", side=1, line=1.7, at=1, adj=.5)
mtext("(right)", 1, 1.7, at=11, adj=.5)
points(ideologia_jitt, vote_jitt, pch=20, cex=.1)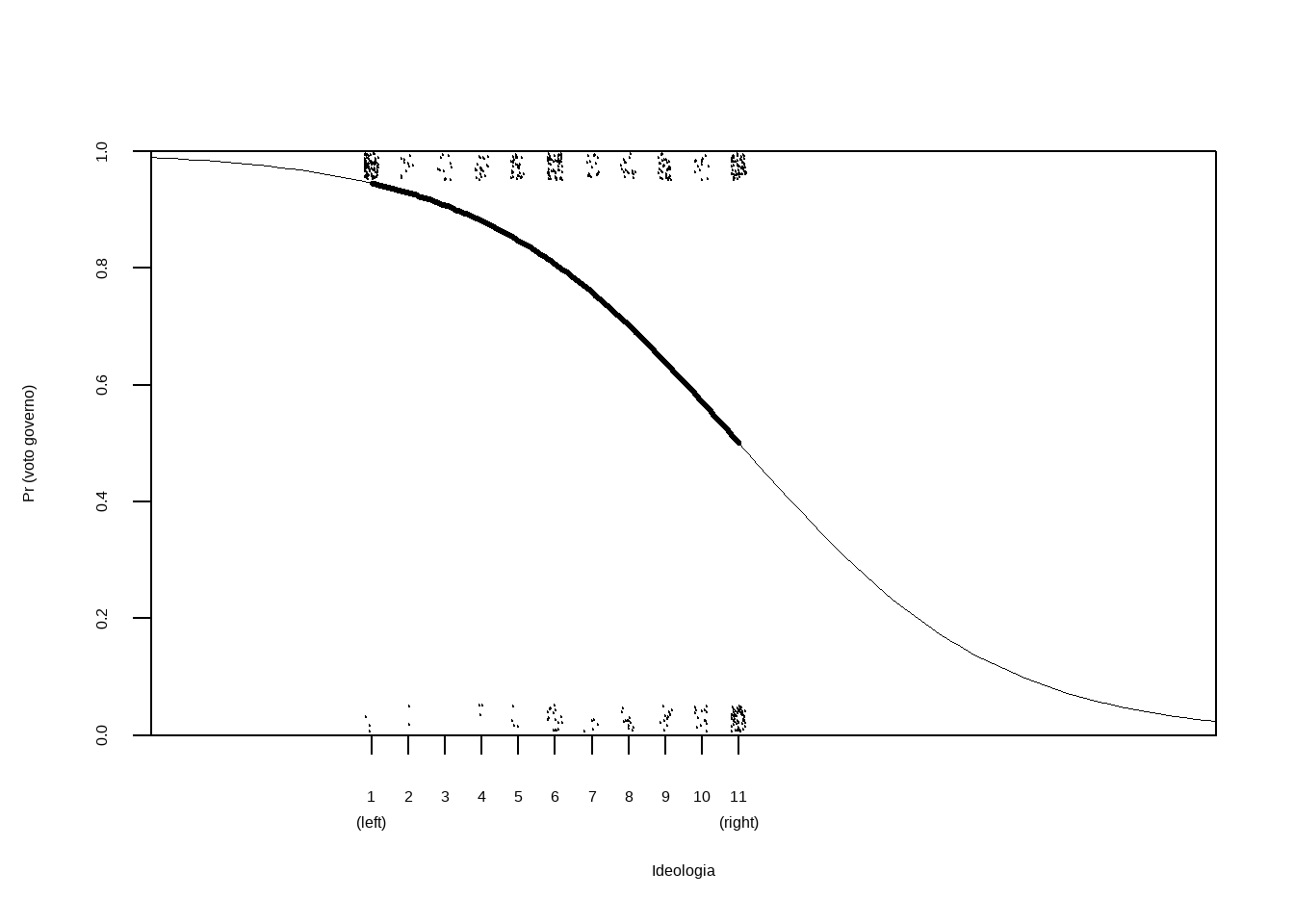
O gráfico apresenta o modelo ajustado da logística, juntamente com os dados (jittered). Cada ponto na curva representa \(Pr(Y=1|X=x)\). A linha mais escura é o modelo ajustado para os pontos da amostra. Podemos observar que há mais dados de pessoas que votariam com o governo entre os indivíduos de esquerda, com mais observações votando contra o governo apenas entre as pessoas mais centristas, o que faz sentido. Também observamos muitas pessoas de direita votando com o governo, indicando que entre as pessoas de direita, o dado não diferencia tanto quem vota a favor ou contra o governo, sugerindo que precisamos considerar outras variáveis.
Como a logística é curva, o efeito preditivo de \(x\) sobre a probabilidade \(y=1\) não é constante (ao contrário de regressões lineares). No caso do nosso gráfico, passar de \(1\) para \(2\) na ideologia tem um efeito significativamente menor (de 95% para 93%) do que passar de \(6\) para \(7\) (de 81% para 76%), por exemplo. Para calcular o efeito preditivo nesses casos, fazemos:
newdata <- data.frame(ideologia = 1:11)
previsao <- predict(reg_logistica, newdata =newdata, type = "response")
print(round(previsao, 2))## 1 2 3 4 5 6 7 8 9 10 11
## 0.95 0.93 0.91 0.88 0.85 0.81 0.76 0.70 0.64 0.57 0.50A interpretação do coeficiente é um pouco difícil na logística, mas um caminho é pensar que o efeito é máximo no centro da curva, em que \(\alpha + \beta x = 0\). Nesse caso, a inclinação da curva (a derivada) é dada por \(\beta/4\). Ou seja, podemos dividir o coeficiente estimado por quatro para ter uma ideia do máximo impacto preditivo. Em nosso caso, com um coeficiente aproximado de \(-0,29\), temos que no máximo a mudança em uma unidade diminui a probabilidade em no máximo 7,25%. E nos dados, esse efeito máximo é alcançado quando \(3.14 + -0.29*x = 0\), ou seja, aproximadamente \(x = 11\).
13.2.3 Odds Ratio - Razão de chances
Outra forma de interpretar a regressão logística é utilizando a parametrização do logito. O coeficiente assume a forma de razão de chances, onde uma chance é \(p/(1-p)\), e razão de chances é a divisão de duas chances (o que quer que isso signifique). Uma vantagem de trabalhar com razão de chances é que a interpretação do coeficiente se torna linear, em vez de não-linear, conforme mostra a equação abaixo.
\[ log(\frac{Pr(Y=1|X=x)}{Pr(Y=0|X=x)}) = \alpha + \beta x \]
Eu acho complicado entender o que é uma razão de chances, então preferimos trabalhar com probabilidade. Mas existe essa outra parametrização.
13.3 Logística como variável latente
Uma outra forma de interpretar ou justificar a logística é com a formulação de variável latente. Imagine que existe uma variável latente (não observada), \(z\), que é contínua e reflete a propensão a votar no governo. Porém, nós só observamos os valores \(1\) ou \(0\), de tal modo que podemos escrever:
\[\begin{align} y_i = 1, se & & z_i > 0 \\ y_i = 0, c.c. \\ z_i = \alpha + \beta x_i + e_i, e_i \sim logistica \end{align}\]
A distribuição logística é dada por: \[ Pr(e_i < x) = \frac{\exp(x)}{1 + \exp(x)} \]
Portanto, temos que:
\[\begin{align} Pr(y_i = 1) = Pr(z_i > 0) = \\ Pr(e_i + \alpha + \beta x_i > 0) = \\ Pr(e_i > -\alpha - \beta x_i) \\ \textrm{Pela regra do complemento:} \\ Pr(e_i > -\alpha - \beta x_i) = 1 - Pr(e_i < -\alpha - \beta x_i) = \\ 1 - \frac{\exp(- \alpha - \beta x_i)}{1 + \exp(- \alpha - \beta x_i)} = \\ \frac{1 + \exp(- \alpha - \beta x_i) - \exp(- \alpha - \beta x_i)}{1 + \exp(- \alpha - \beta x_i)} = \\ \frac{1}{1 + \exp(- \alpha - \beta x_i)} \tag{13.2} \end{align}\]
Vimos assim que as parametrizações de (13.1) e (13.2) são equivalentes.
13.4 Probit
Se, por outro lado, supusermos que o termo de erro tem distribuição normal, em vez de distribuição logística, teremos um modelo probit.
\[ z_i = \alpha + \beta x_i + e_i, e_i \sim N(0, \sigma^2) \] Quando \(\sigma = 1.6\), essa formulação é aproximadamente a regressão logística. Isso significa que o coeficiente da probit é aproximadamente o da logística/1.6 e vice-versa, isto é, podemos multiplicar o coeficiente da probit por 1.6. Vamos checar no R.
reg_logistica <- glm(votaria_governo ~ ideologia, data=br_latbar_23,
family=binomial(link= "logit"))
reg_probit <- glm(votaria_governo ~ ideologia, data=br_latbar_23,
family=binomial(link= "probit"))
library(stargazer)
stargazer(reg_logistica, reg_probit, type = "html")| Dependent variable: | ||
| votaria_governo | ||
| logistic | probit | |
| (1) | (2) | |
| ideologia | -0.285*** | -0.165*** |
| (0.039) | (0.021) | |
| Constant | 3.140*** | 1.836*** |
| (0.338) | (0.178) | |
| Observations | 472 | 472 |
| Log Likelihood | -239.376 | -239.128 |
| Akaike Inf. Crit. | 482.753 | 482.256 |
| Note: | p<0.1; p<0.05; p<0.01 | |
13.5 Logística como GLM
Uma outra forma de pensar a logística é como um modelo linear generalizado. Nós vimos que o modelo linear precisou entrar em uma função \(f\) que transformasse os intervalos entre \(0\) e \(1\). Podemos considerar o modelo de regressão linear como um caso particular, em que temos a função identidade \(f(x) = x\) e a distribuição da resposta é modelada como Gaussiana. Na logística,a função de ligação é logística, e a resposta modelada como Bernoulli (e para \(n\) dados, binomial).
Similarmente, se tenho dados discretos \(\{1, 2, 3, ..., n\}\), posso modelar meus dados com uma Poisson e com uma função \(f\) específica, que chamamos de função de ligação.
13.6 Logística com múltiplos preditores
reg_logistica1 <- glm(votaria_governo ~ ideologia + evangelico, data=br_latbar_23,
family=binomial(link= "logit"))
reg_logistica1 %>%
tidy() %>%
kable()| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 3.3035245 | 0.3498086 | 9.443805 | 0.0000000 |
| ideologia | -0.2780476 | 0.0391497 | -7.102157 | 0.0000000 |
| evangelico | -0.7387838 | 0.2432515 | -3.037120 | 0.0023885 |
Para facilitar a comparação de coeficientes, pode ser mais fácil padronizar as variáveis. No caso, vamos padronizar apenas ideologia (precisamos supor que é uma variável contínua, medida com valores discretos).
br_latbar_23 <- br_latbar_23 %>%
mutate(ideologia_pad = (ideologia - mean(ideologia))/sd(ideologia))
reg_logistica2 <- glm(votaria_governo ~ ideologia_pad + evangelico, data=br_latbar_23,
family=binomial(link= "logit"))
reg_logistica2 %>%
tidy() %>%
kable()| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 1.4449650 | 0.1497791 | 9.647304 | 0.0000000 |
| ideologia_pad | -0.9975056 | 0.1404511 | -7.102157 | 0.0000000 |
| evangelico | -0.7387838 | 0.2432515 | -3.037120 | 0.0023885 |
Usando a regra de dividir por quatro, temos que: ideologia tem efeito máximo de redzir a probabilidade em 25%, e evangélico de diminuir em 18%.
Plotando graficamente os dois preditores, temos:
jitter_binary <- function(a, jitt=0.05){
ifelse(a==0, runif(length(a), 0, jitt), runif(length(a), 1 - jitt, 1))
}
br_latbar_23$votaria_governo_jitter <- jitter_binary(br_latbar_23$votaria_governo)
ideologia_jitt <- br_latbar_23$ideologia_pad + runif(n, -.05, .05)
plot(ideologia_jitt, br_latbar_23$votaria_governo_jitter, xlim=c(0,max(ideologia_jitt)))
curve(invlogit(cbind(1, x, 0) %*% coef(reg_logistica2)), add=TRUE)
curve(invlogit(cbind(1, x, 1.0) %*% coef(reg_logistica2)), add=TRUE)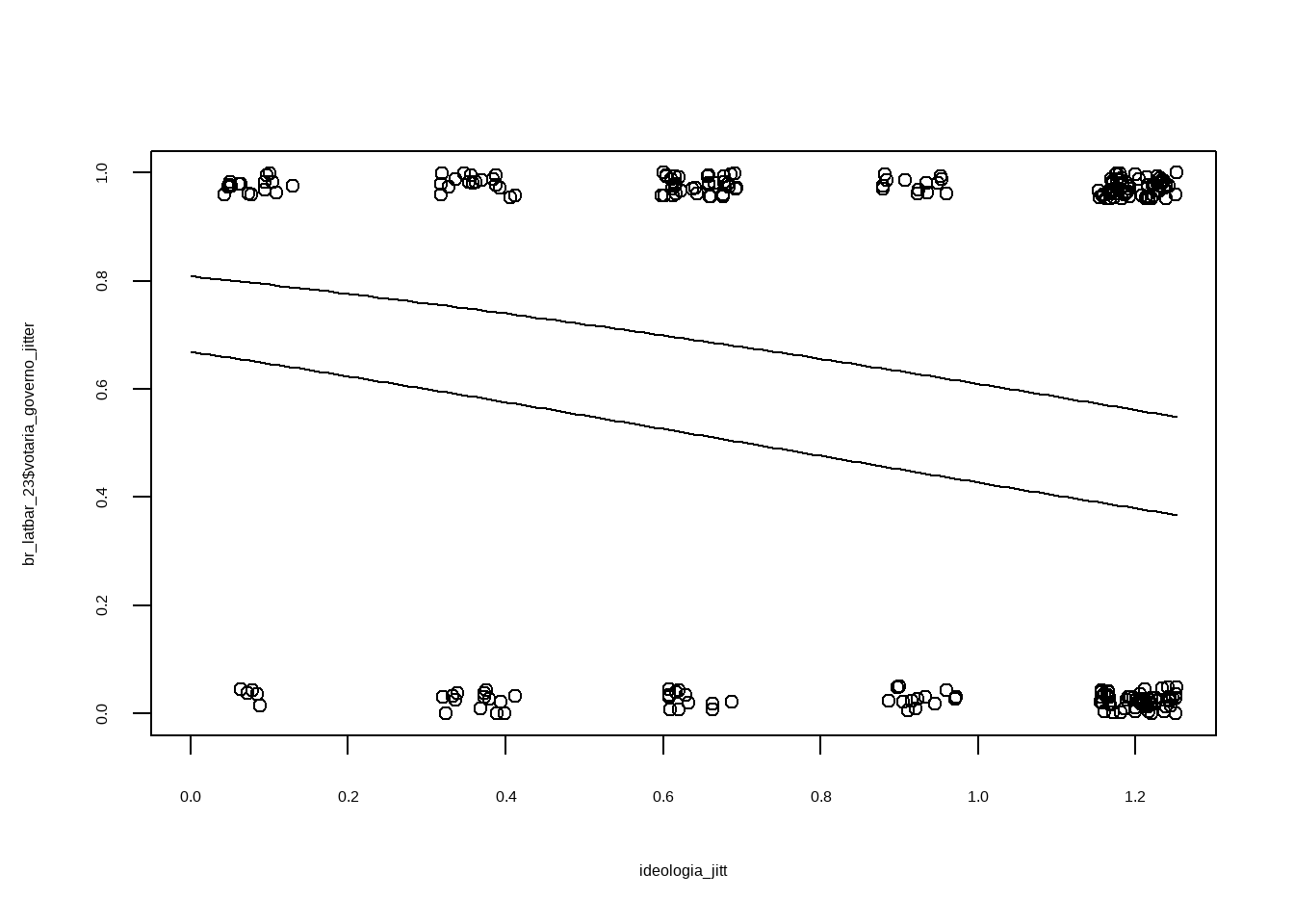
13.7 Ajuste do modelo
Nós vimos que podemos usar o erro quadrático médio com regressão linear para comparar ajustes do modelo. Porém, para variáveis binárias, há formas melhores de comparar a capacidade preditiva do modelo. A mais tradicional é o log da verossimilhança, dado pela soma para todos as observações de: \((ylog(p) + (1-y)log(1-p))\). No limite, um modelo perfeito, que classifica corretmente todas as observações (isto é, coloca probabilidade \(1\) de sucesso e \(0\) de fracasso) teria um log da verossimilhança igual a zero. Portanto, quanto mais próximo de zero, melhor o ajuste do modelo. E um modelo “burro”, que previsse probabilidade de 50% para cada ponto, teria um total de \(n \cdot log(.5) = n \cdot -0.693\). Um modelo um pouco melhor seria um que previsse a média, isto é, se 60% dos casos são sucesso, pode prever para todas as observações \(p=.6\). Esses modelos simples servem como comparação. No R:
y_hat <- predict(reg_logistica, type="response")
y_obs <- br_latbar_23$votaria_governo
log_likelihood <- sum(y_obs*log(y_hat) + (1-y_obs)*log(1 - y_hat))
print(log_likelihood)[1] -239.3764
[1] -274.8595
[1] -327.1655
| Dependent variable: | ||
| votaria_governo | ||
| (1) | (2) | |
| ideologia | -0.285*** | -0.278*** |
| (0.039) | (0.039) | |
| evangelico | -0.739*** | |
| (0.243) | ||
| Constant | 3.140*** | 3.304*** |
| (0.338) | (0.350) | |
| Observations | 472 | 472 |
| Log Likelihood | -239.376 | -234.816 |
| Akaike Inf. Crit. | 482.753 | 475.632 |
| Note: | p<0.1; p<0.05; p<0.01 | |
Para mais detalhes sobre regressão logística, nossa referência favorita é o livro de Gelman, Hill e Vehtati, Regression and other Stories, de onde tiramos alguns dos códigos do presente capítulo. Capítulos 13 e 14 contém bastante material a um nível que exige um nível de matemática similar ao que temos usado em nosso livro.
13.8 Regressão com dados Ordenados
Até agora tratamos de variáveis respostas binárias. Porém, Há outros tipos de dados categóricos além de binários, e passamos agora a apresentar como tratar desses dados. A aboragem escolhida aqui é aquela de modelos de escolha discreta, que é uma extensão da abordagem de variável latente que vimos acima para regressão logística.
A ideia é que existe uma probabilidade que o indivíduo \(i\) escolha a alternativa \(j\) (de um conjunto discreto e mutuamente excludente de \(J\) alternativas, daí o nome de escolhas discretas), \(p_{ij}\). Como anteriormente, a relação entre a probabilidade e os preditores é dada por uma função de ligação \(f(u)\) e \(u = X_ij\beta\), ou seja, uma modelo linear das variáveis preditoras e \(u\). E vamos considerar que podemos ordenar nossa variável resposta, isto é, que as opções possam ser consideradas como um conjunto ordenado.
Exemplos de variáveis respostas incluem escalas likerts (discordo muito, discordo pouco, concordo pouco, concordo muito), escalas discretas de ideologia, em que os extremos vão da esquerda à direita, votação em que consideramos não, abstenção e sim, assinar um tratado sem reservas, com reservas ou não assinar, e assim por diante.
Seguindo com a formulação de variável latente, podemos pensar que existe uma variável \(z\), não observada, tal que:
\(z_i = X_{ij}\beta + e\). Supondo, para ilustrar, que tenhamos \(4\) categorias ou opções, como no exemplo da escala Likert, então temos \(J=4\) categorias ordenadas de \(1-4\), e o que nós observamos é uma escolha a dependenter de \(J-1=3\) pontos de corte, \(\tau_1, \tau_2, \tau_3\):
\[ z = \begin{cases} 1 & \text{se } z \leq \tau_1 \\ 2 & \text{se } \tau_1 < z \leq \tau_2 \\ 3 & \text{se } \tau_2 < z \leq \tau_3 \\ 4 & \tau_3 < z \end{cases} \]
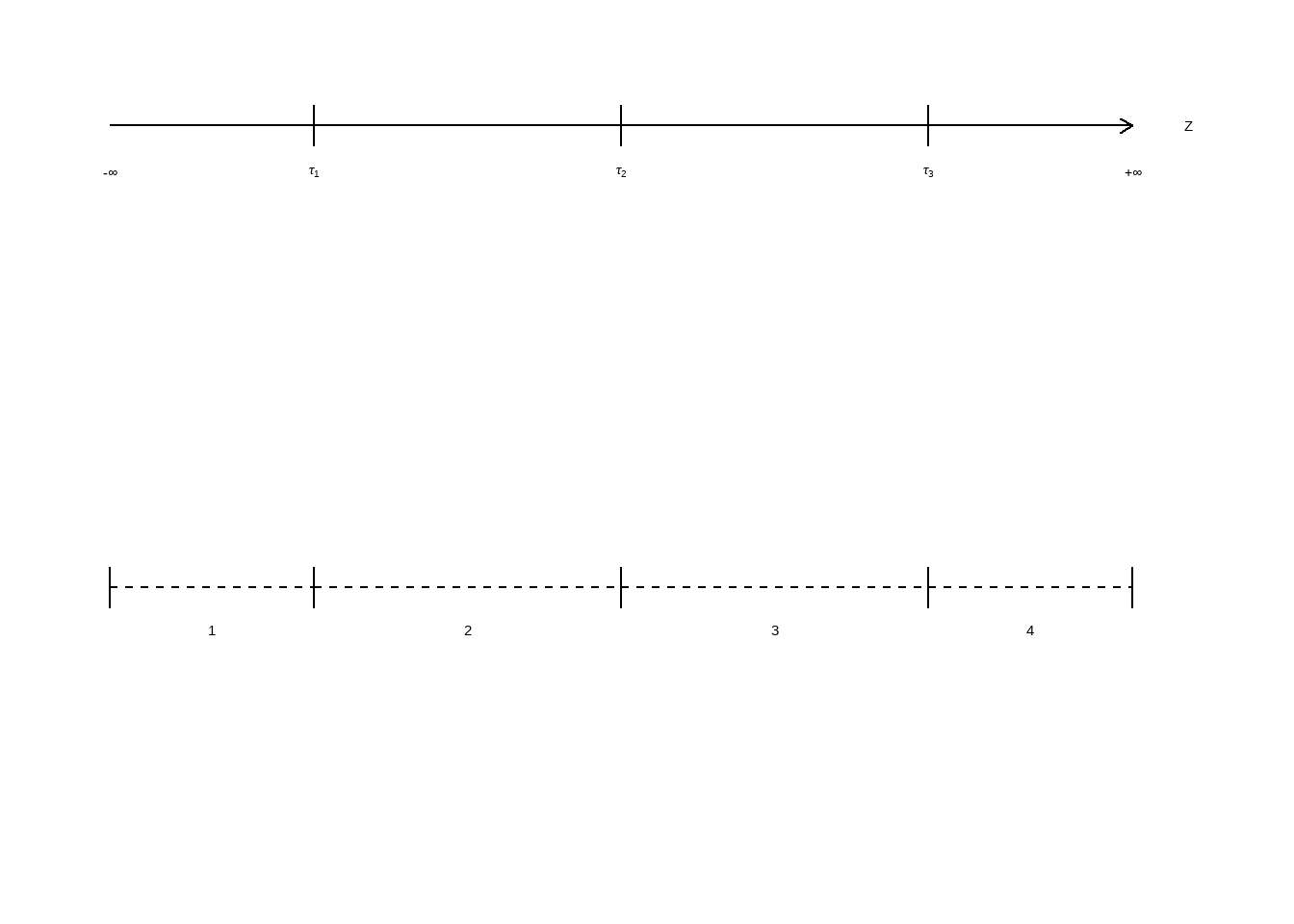
Figure 13.1: Mapa entre Z e Y
Vejam que nesse modelo, além dos coeficientes da regressão, também temos de estimar os pontos de corte dados pelos parâmetros de \(\tau_1\) a \(\tau_3\). De fato, a probabilidade de escolhermos a primeira categoria, é: \[Pr(Y_i = 1) = Pr(Z_i \leq \tau_1) = Pr(X_{ij}\beta + e \leq \tau_1) = Pr(e \leq \tau_1 - X_{ij}\beta)\] Similarmente, a probabilidade de um respondente escolher a segunda categoria é:
\[Pr(Y_i = 2) = Pr( \tau_1 < Z_i \leq \tau_2) = Pr(\tau_1 < X_{ij}\beta + e \leq \tau_1) = Pr(\tau_1 - X_{ij}\beta < e \leq \tau_1 - X_{ij}\beta)\]
Se supusermos que \(e\) tem distribuição logística com média zero e variância \(\frac{\pi^2}{3}\), que é a logística padrão, temos o modelo de regressão logística ordenado. Se supusermos que o erro tem distribuição normal, com média zero e variância 1, temos o modelo probit ordenado. Vejamos um exemplo simulado e em seguida uma aplicação empírica.
Em nossa simulação, vamos supor que um survey foi rodado e medimos, usando uma escala likert com quatro opções, se a pessoa concorda ou não com uma dada frase. Podemos pensar que a variável latente \(z\) é a propensão a concordar com a frase, e só observamos uma das quatro categorias.
#
library(tidyverse)
set.seed(1234)
n <- 1000 # número de indivíduos
m <- 4 # número de alternativas (discordo muito, pouco, concordo pouco, muito)
x_subject <- rnorm(n)
erro <- rlogis(n, location = 0, scale = 1)
beta_0 <- .5
beta1 <- 2
z <- beta_0 + beta1*x_subject + erro
tau1 <- -2
tau2 <- 1
tau3 <- 4
y <- ifelse(z <= tau1, "discordo muito",
ifelse(z <= tau2, "discordo pouco",
ifelse(z <= tau3, "concordo pouco", "concordo muito")))
df <- data.frame(y=y, x1 = x_subject)
df <- df %>%
mutate(y = factor(y, ordered=T))
# checando a ordem
levels(df$y)## [1] "concordo muito" "concordo pouco" "discordo muito" "discordo pouco"# ordem trocada (inversa)
#vamos corrigir
df <- df %>%
mutate(y = factor(y, levels = c("discordo muito",
"discordo pouco",
"concordo pouco",
"concordo muito"),
ordered=T))
# checando a ordem
levels(df$y)## [1] "discordo muito" "discordo pouco" "concordo pouco" "concordo muito"## [1] TRUE## formula: y ~ x1
## data: df
##
## link threshold nobs logLik AIC niter max.grad cond.H
## logit flexible 1000 -896.27 1800.54 6(0) 6.70e-09 7.9e+00
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## x1 2.15892 0.09835 21.95 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Threshold coefficients:
## Estimate Std. Error z value
## discordo muito|discordo pouco -2.62133 0.12144 -21.586
## discordo pouco|concordo pouco 0.33123 0.08152 4.063
## concordo pouco|concordo muito 3.55039 0.15692 22.625A primeira forma de interpretar os coeficientes é que se o \(\beta\) é positivo, quanto maior o valor do preditor, maior a propensão a concordar com a frase e vice-versa se for negativo. Isso é fácil de ver na formulação da variável latente. Para analisar as probabilidades de cada categoria precisamos olhar também os pontos de corte.
Vejam que os coeficientes dos pontos de corte estão “errando” por aproximadamente meio em relação aos parâmetros. Isso é porque o modelo não estima intercepto. Se rodarmos a simulação de novo com \(\beta_0 = 0\), iremos nos aproximar dos verdadeiros pontos de corte. A razão é que não é possível identificar um intercepto distinto do valor de \(\tau\), ou seja, é como se tivéssemos subtraído \(.5\) de todos os \(\tau\) e rodado o modelo sem intercepto. Em too caso, vamos interpretar os pontos de corte estimados.
O que eles nos dizem, em conjunto com o \(\beta\), é a probabilidade de uma pessoa escolher uma dada categoria.