Capítulo 4 Introdução à Simulação
4.1 Objetivos
Entender o que é um Processo Gerador de Dados (DGP) e como especificá-lo em R.
Gerar amstras aleatórias de distribuições (rnorm, runif, rbinom, rpois, …) e fixar semente com set.seed().
Compreender simulação de Monte Carlo: por que, quando e como.
Realizar aplicações de simulação, como diferenciar LLN (Lei dos Grandes Números) e CLT (Teorema Central do Limite) via simulação; e entender cobertura de intervalos de confiança (IC) e avaliar coberturas para níveis 80/90/95/99% com gráficos.
4.2 Introdução
Simulação é uma ferramenta extremamente importante em probabilidade e estatística. Dois são seus principais usos. De um lado, é possível usar um modelo de probabilidade para recriar, artificialmente, no computador, amostras desse modelo, quantas vezes quisermos. Tudo se passa como se tivéssemos o poder de criar um mundo, totalmente controlado por nós, e podemos simular esse mundo e verificar o que acontece. Isso é útil quando não podemos ou não queremos verificar matematicamente o que deveria acontecer com base no modelo matemático de probabilidade. De outro lado, é possível usar simulações para aproximar quantidades matemáticas que não podemos ou não queremos calcular analiticamente. Por calcular analiticamente, é fazendo a conta nós mesmos. Um exemplo simples disso é, em vez de calcular os resultados de alguma análise combinatória usando as fórmulas de combinação e simularmos os valores e contar quantas combinações resultam.
No geral usamos simulação para o primeiro tipo de uso. Mas, aqui no curso, será útil que vocês verifiquem resultados matemáticos por meio de simulações. Assim, se escrevemos que \(\sum_{i=1}^{10} i = 55\), vocês podem verificar com código no R essa soma, por exemplo, rodando: sum(1:10). Sempre que vocês tiverem dúvida de algum passo matemático, podem fazer uma simulação para entender melhor o que está acontecendo. Isso é encorajado, para melhorar a intuição do que está acontecendo e lhe assegurar que de fato você está entendendo o que está acontecendo. Podemos usar simulações para aproximar quantidades. Um exemplo clássico em probabilidade é a fórmula de Stirling, dada por \(n! \sim \sqrt{2\pi}n^{n + 1/2}*e^{-n}\). Então, por exemplo, \(10! = 10*9*8*7*6*5*4*3*2*1\) com os computadores modernos pode ser calculada diretamente para números não tão grandes. No caso, \(10! = 3628800\). Ou pode ser aproximada pela fórmula de Stirling:
Exemplo 4.1
# especificando semente, para simulação ser reproduzível
set.seed(2)
# número de amostras
stirling_aprox <- function(n) {
sqrt(2*pi)*n^(n+1/2)*exp(-n)
}
print(stirling_aprox(10))[1] 3598696
[1] 0.991704
[1] 0.00829596
Como se vê, a fórmula de Stirling é bem precisa para aproximar fatorial e muito mais fácil de computar.
4.3 DGP — Processo Gerador de Dados
Definição (intuitiva): um DGP descreve como os dados são produzidos na população. Tipicamente contém um componente determinístico e outro estocástico.
Origem do termo “estocástico”
Estocástico possui origem grega, stókhos. Referia-se à capacidade de adivinhar ou conjecturar. Em latim, o termo aproximadamente equivalente é alea, como na famosa frase de Júlio Cesar, “Alea iacta est”, quando decidiu atravessar o Rubicão. Comumente traduzido por “a sorte está lançada”, mas aparentemente seria melhor algo como “os dados estão lançados”, sendo os dados aleatórios.
Em resumo, temos duas palavras com significados similares (estocástico e aleatório). O inglês random aparentemente vem do francês randon, querendo dizer impetuoso, desorganizado, e utilizado pelo seu derivado randonné, que tem a ver com trilha ou caminhada desorganizada, caótica, bagunçada. Portanto, nada de usar “randomizar” quando podemos utilizar aleatorizar com o mesmo significado.
Fonte: math.stackexchange.com
Por hora, vamos trabalhar com DGPs apenas estocásticos.
Um DGP estocástico é tipicamente definido por uma distribuição de probabilidade (Normal, Bernoulli, Poisson, Exponencial etc.) e os parâmetros que govenram a distribuição: média/variância (Normal), probabilidade (Bernoulli), taxa (Poisson/Exponencial). Às vezes a distribuição de probabilidade pode ser reparametrizada (por exemplo, especificar a Normal em termos do desvio-padrao em vez da variância, ou o inverso da variância, chamado de precisão).
É preciso definir também a relação entre os dados, se de Independência/Identicamente distribuídos (i.i.d.) ou se há presença de dependência (séries temporais, agrupamentos espaciais etc.).
4.4 Simulação de Monte Carlo
A simulação de Monte Carlo é um método computacional que se utiliza de amostras repetidas de um dado DGP para nos permitir calcular determinadas quantidades númericas. O nome vem do principado de Mônaco, com seus cassinos e jogos de azar, e foi criado nos anos 40 em Los Alamos, para auxiliar nos cálculos necessários para construção da bomba atômica. Em estatística, as quantidade calculadas são chamadas de “estatísticas”.
Estatística
Uma estatística é qualquer quantidade calculada a partir de uma amostra e utilizada para um propósito estatístico. Exemplos são a média (amostral), variância, desvio-padrão, mediana. Mas também estatística T, Z, F etc. Quando calculamos uma estatística para estimar um parâmetro de um modelo, chamamos essa estatística de estimativa. E o método de estimador.
Para realizar uma simulação ou experimento de Monte Carlo, especificamos o DGP, tamanho amostral, definimos a semente para garantir a reprodutibilidade e então o resumo e visualização da distribuição empírica da estatística.
Pergunta: Por que usamos set.seed() antes de simular?
4.4.1 Simulando um dado
Comecemos lembrando que probabilidades podem ser interpretadas como frequências relativas de longo prazo. Portanto, a probabilidade de um evento pode ser aproximada por simulações, na medida em que aproximamos a frequência relativa com que o fenômeno acontece em nossas simulações. Vamos dar um exemplo simples desse tipo de aplicação.
Suponha que quero simular a probabilidade do número 6 sair em um dado de seis lados.
Exemplo 4.1.1
# especificando semente, para simulação ser reproduzível
set.seed(234)
# número de amostras
n <- 10000
# 1000 amostras de uma lançamento de dado de 6 lados
resultado <- sample(1:6, n, TRUE)
# frequência relativade 6 é dada por número de 6 / total de amostras
prob_6 <- sum(resultado == 6)/n
# 16,89%
# 1/6 = 16.6666Podemos também ver como a aproximação converge para o verdadeiro valor à medida que \(n\) cresce.
# especificando semente, para simulação ser reproduzível
set.seed(234)
# número de amostras
vec_amostra <- c(100, 1000, 10000, 100000, 1000000)
# lista vazia para armazenar os resultados das simulações
resultado_lista <- list()
# vetor vazio para armazenar a frequência relativa de 6
vec_prob6 <- numeric()
set.seed(234)
# loop sobre os tamanhos das amostrar
for ( i in 1:length(vec_amostra)) {
# n amostras de uma lançamento de dado de 6 lados
resultado_lista[[i]] <- sample(1:6, vec_amostra[i], TRUE)
# frequência relativade 6 é dada por número de 6 / total de amostras
vec_prob6[i] <- sum(resultado_lista[[i]] == 6)/vec_amostra[i]
}
print(vec_prob6)[1] 0.150000 0.189000 0.164700 0.169250 0.166257
Se supusermos que todos os números possuem a mesma chance de sair quando jogamos os dados, então, a distribuição conjunta de \(X\) e \(Y\) pode ser dada por:
library(knitr)
library(kableExtra)
# Definir os valores de (x, y) e P(X = x, Y = y)
valores <- c("(2, 1)", "(3, 2)", "(4, 2)", "(4, 3)", "(5, 3)", "(5, 4)", "(6, 3)", "(6, 4)", "(7, 4)", "(8, 4)")
probabilidades <- c(0.0625, 0.1250, 0.0625, 0.1250, 0.1250, 0.1250, 0.0625, 0.1250, 0.1250, 0.0625)
# Criar a tabela
tabela <- data.frame("(x, y)" = valores, "P(X = x, Y = y)" = probabilidades)
# Formatar a tabela
kable(tabela, caption = "Tabela 2.26: Tabela representando a distribuição conjunta da soma (X) e o maior (Y) de dois lançamentos de um dado de quatro faces",
col.names = c("$(X,Y)$", "$P(X=x, Y=y)$")) %>%
kable_styling(bootstrap_options = "striped")| \((X,Y)\) | \(P(X=x, Y=y)\) |
|---|---|
| (2, 1) | 0.0625 |
| (3, 2) | 0.1250 |
| (4, 2) | 0.0625 |
| (4, 3) | 0.1250 |
| (5, 3) | 0.1250 |
| (5, 4) | 0.1250 |
| (6, 3) | 0.0625 |
| (6, 4) | 0.1250 |
| (7, 4) | 0.1250 |
| (8, 4) | 0.0625 |
como podemos ver, à medida que \(n\) cresce, a simulação converge para o verdadeiro valor do parâmetro, embora isso não seja linear. Por isso que é importante variar a configuração para ter certeza de que a simulação está próxima do verdadeiro valor do parâmetro.
De maneira geral, uma simulação envolve os seguintes passos.
4.5 Configuração
Definir o modelo de probabilidade, variáveis aleatórias e eventos a serem modelados. O modelo de probabilidade codifica todas as suposições do modelo. No exemplo acima, de que todos os lados têm a mesma probabilidade de sair, que existem apenas seis possibilidades, numeradas de \(1-6\) e assim por diante.
4.6 Simular
Vamos considerar o exemplo dos dados novamente. Vamos usar a função sample para simular lançamento de um dado de quatro faces.
Para “jogar o dado” uma vez, sorteio um número entre 1 e 4.
Como quero a frequência de longo prazo, preciso repetir esse processo (de maneira independente a cada jogada) \(n\) vezes.
# número de jogadas/simulações
n <- 1000
# vetor X, para armazenar o resultado de cada uma das n jogadas
X <- numeric()
# simulando n vezes
for( i in 1:n){
X[i] <- sample(1:4, size=1)
}
# visualizando as primeiras 20 jogadas
head(X, 20)[1] 4 4 1 4 2 3 2 4 2 2 3 4 4 1 4 2 4 2 3 3
4.7 Resumir
Após realizada a simulação, queremos não olhar todos os números simulados, mas resumir a simulação. Por exemplo, obtendo a minha distribuição de probabilidade, ou a esperança.
[1] 0.262
[1] 0.26
[1] 0.232
[1] 0.246
Min. 1st Qu. Median Mean 3rd Qu. Max. 1.000 1.000 2.000 2.462 3.000 4.000
Questão:
O que faz o código replicate(10000, { … })?
4.8 LGN e TCL
Qual a diferença entre a Lei dos Grandes Números e o Teorema Central do Limite? Uma forma de entender esses dois resultados fundamentais é por meio de simulações. Vamos simular o LGN e depois o TCL
library(knitr)
library(ggplot2)
library(tidyverse)
set.seed(123)
n_values <- c(5, 10, 30, 50, 100, 200, 300, 400, 500, 1000, 2000, 3000, 4000, 5000, 10000, 20000, 30000, 40000, 50000)
s_means <- numeric()
for(i in 1:length(n_values)) {
s_means[i] <- mean(rnorm(n_values[i], mean = 100, sd = 15))
}
df <- data.frame(n = n_values, sample_mean = s_means)
kable(df)| n | sample_mean |
|---|---|
| 5 | 102.90355 |
| 10 | 101.97687 |
| 30 | 100.36523 |
| 50 | 101.25004 |
| 100 | 98.73293 |
| 200 | 100.60105 |
| 300 | 99.51731 |
| 400 | 101.08235 |
| 500 | 100.19364 |
| 1000 | 100.07918 |
| 2000 | 99.81436 |
| 3000 | 99.99797 |
| 4000 | 100.08209 |
| 5000 | 99.88526 |
| 10000 | 99.66418 |
| 20000 | 99.99947 |
| 30000 | 100.17037 |
| 40000 | 100.07525 |
| 50000 | 100.01786 |
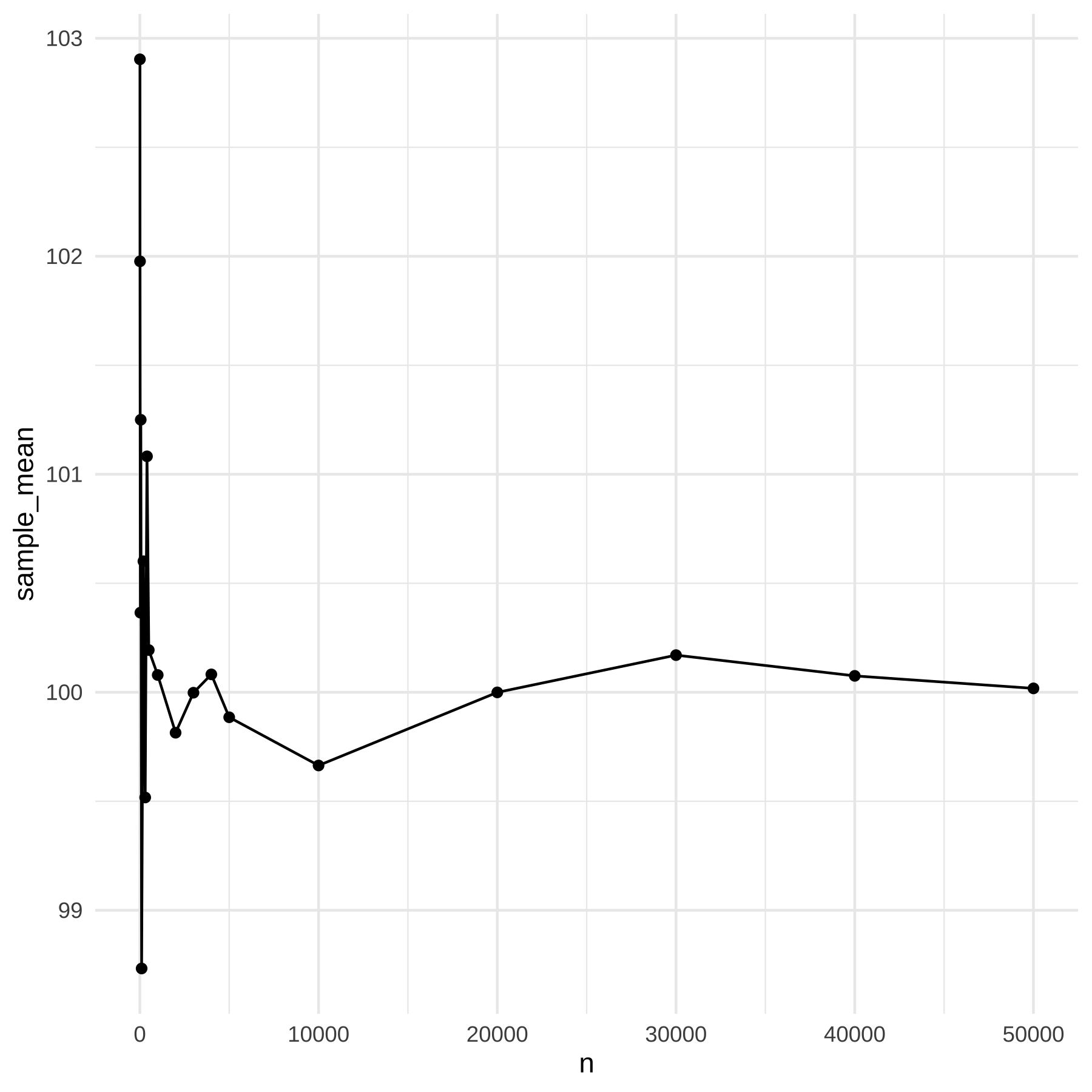
Pergunta:
A LGN diz que a média amostral iguala a média populacional quando \(n\) é grande, ou apenas que se aproxima da média populacional?
Definição do TCL:
Se você coletar muitas amostras independentes de tamanho \(n\) de uma população com qualquer distribuição de probabilidade, mas com variância finita, então a distribuição da médioa amostral será aproximadamente normal quando \(n\) é grande.
Exemplo de uma simulação com distribuição oginal da variável aleatória uniforme:
set.seed(123)
means <- replicate(10000, mean(runif(36, min = 0, max = 1)))
hist(means, main = "Distribution of sample means", xlab = "Mean", breaks = 30)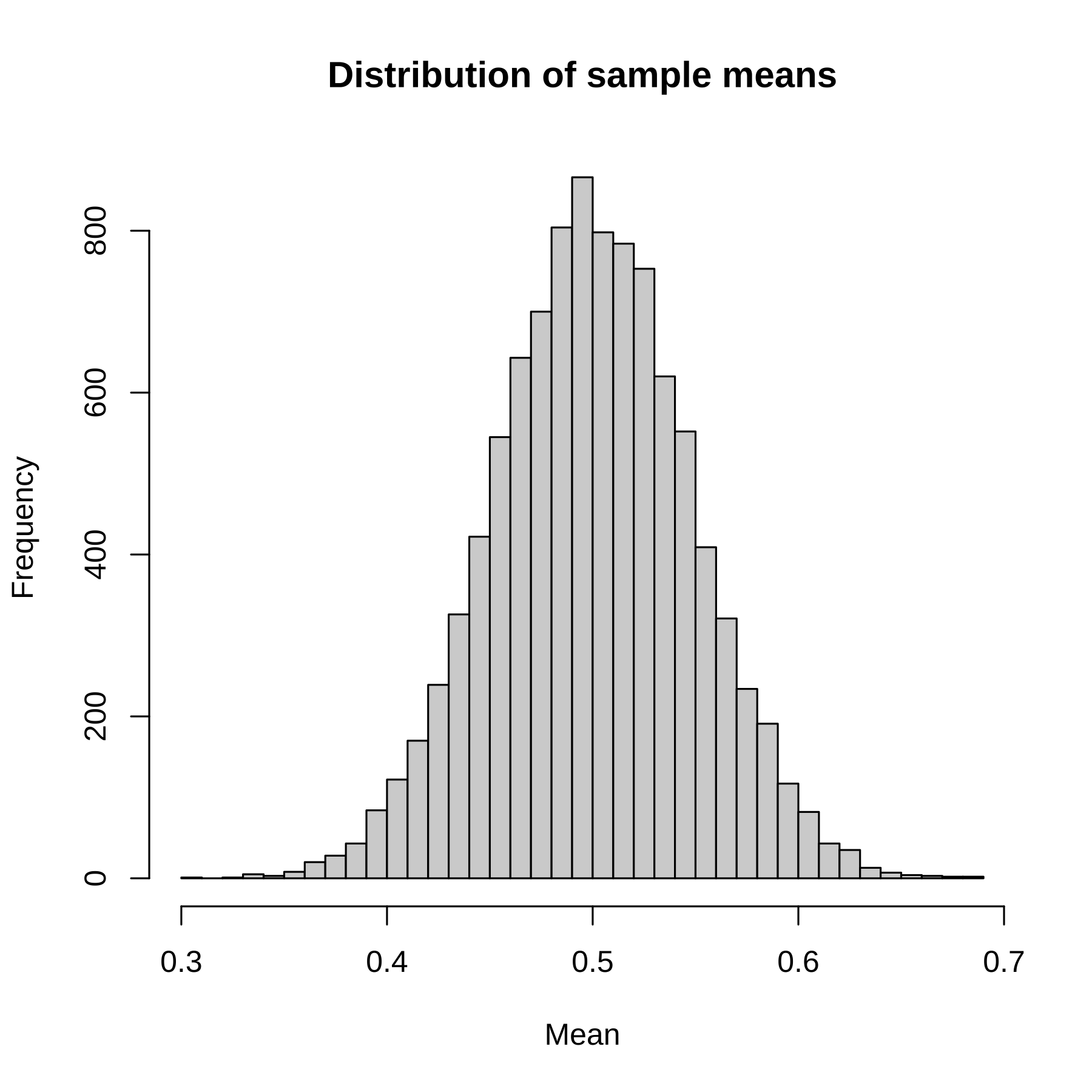
Qual a média e o desvio-padrão da distribuição da média amostral?
Podemos calcular aproximadamente a partir de nossa simulação. A média da simulação é 0.5000232 e o desvio-padrão é 0.048084. Vejam que a média amostral é próxima da média populacional e o desvio-padrão amostral é próximo do desvio-padrão populacional dividido pela raiz-quadrada de \(n\). Lembrando que a variância de uma uniforme é dada por \(\frac{1}{12}(a - b)^2\), em que \(a\) é o maior valor e \(b\) o menor. Logo, em nosso caso, a variância é \(\frac{1}{12}(1 - 0)^2 = 1/12\). E o desvio-padrão é a raiz quadrada disso, ou \(0.2886751\). Como \(n = 36\), a raiz-quadrada é \(6\), ou seja, igual a \(0.2886751/6 = 0.04811252\).
4.9 Cobertura de um IC
Um Intervalo de Confiança (IC) de 95% possui uma cobertura nominal de 95%. O que isso quer dizer? Quer dizer que se repetirmos o procedimento infinitas vezes, em 95% delas o IC conterá o verdadeiro valor do parâmetro. Vamos verificar isso com uma simulação.
set.seed(123)
n_sims <- 10000
n <- 30
true_mean <- 50
true_sd <- 10
cover <- replicate(n_sims, {
x <- rnorm(n, mean = true_mean, sd = true_sd)
se <- sd(x)/sqrt(n)
ci_lower <- mean(x) - 1.96*se
ci_upper <- mean(x) + 1.96*se
(true_mean >= ci_lower) & (true_mean <= ci_upper)
})
mean(cover) # proportion of CIs containing true mean[1] 0.9461
Nessa simulação, nós rodamos 10.000 vezes a simulação e calculamos o intervalo de confiança para a média em cada iteração. Ao final, comoutamos o percentual de vezes em que o CI continha o verdadeiro valor do parâmetro. Veja que nesse exemplo não foi exatamente 95%, mas 94.61%. Cmo sempre, a simulação nos dá uma resposta aproximada, não exata.