Capítulo 11 - Inferencia
Nós já trabalhamos com um modelo de regressão em que supomos normalidade do termo de erro e isso permitiu calcular o estimador de máxima verossimilhança e fazer inferência desse estimador de máxima verossimilhança. Contudo, a suposição de normalidade do erro é bastante restritiva, já que se isso não for verdade nem aproximadamente, não poderemos fazer inferência. Isso é particularmente relevante em amostras finitas (pequenas), onde não poderemos contar com alguma versão do Teorema Central do Limite para justificar a suposição de normalidade.
Assim, queremos ser capazes de realizar testes de hipótese, calcular o intervalo de confiança (IC) e também quantificar a incerteza de nossas estimativas por meio do cálculo do p-valor. Aqui não é o lugar para discutir os problemas de misturar o paradigma de teste de hipótese de Neyman-Pearson, com o cálcul do p-valor do Fisher. Basta dizer que essas duas abordagens não se misturam muito bem, mas na prática os pesquisadores as têm combinado como se não houvesse nenhum problema e irei assumir essa mesma postura aqui. Mas o leitor fique avisado que há inconsistências em combinar ambas as abordagens e que ideialmente deveríamos utilizar apenas uma delas.
11.1 Normal
Nós já vimos o caso mais simples em que podemos supor que os erros são normalmente distribuídos, isto é \(e \sim N(0, \sigma^2)\).
Nós vimos também que o meu estimador pode ser decomposto no parâmetro populacional mais uma média ponderada dos erros: \[ \hat{\beta} = \beta + \sum_{i=1}^{n} w_i \cdot e_i \] Ou seja, nosso estimador é igual a uma constante mais uma soma ponderada de variáveis aleatórias normais. E nós sabemos que a soma de variáveis aleatórias normais é uma normal, cuja média é \(\beta\), já que o estimador é não-viesado e sua esperança é o parâmetro populacional e a variância nós também já calculamos e é dada por \(\frac{\sigma^2}{n \cdot S^2_x}\)
Se eu normalizar meu estimador, isto é, subtrair sua média e dividir pelo desvio-padrão amostral, tenho que o estimador normalizado segue a distribuição Normal padrão. Formalmente,
\[ z = \frac{\hat{\beta} - \beta}{\sqrt{\frac{\sigma^2}{n \cdot S^2_x}}} = \frac{\hat{\beta} - \beta}{\frac{\sigma}{\sqrt{n \cdot S^2_x}}} \sim N(0,1 ) \]
Em que \(S^2_x\) é a variância amostral de \(X\) e \(se[\hat{\beta}] = \sqrt{\frac{\sigma^2}{n \cdot S^2_x}}\) é o erro padrão do \(\hat{\beta}\).
Vejam também que:
\[ \frac{\hat{\beta} - \beta}{\sigma} \sim N(0, \frac{1}{n \cdot S^2_x} ) \]
Com isso pudemos realizar testes de hipótese, da seguinte maneira: \[\begin{align*} \mathrm{P}(\beta - 1.96 \cdot se[\hat{\beta}] \le \hat{\beta} \le \beta + 1.96 \cdot se[\hat{\beta}] ) \\ = \mathrm{P}( -1.96 \cdot se[\hat{\beta}] \le \hat{\beta} - \beta \le 1.96 \cdot se[\hat{\beta}] ) \\ = \mathrm{P}( -1.96 \le \frac{\hat{\beta} - \beta}{se[\hat{\beta}]} \le 1.96 ) \\ = \Phi(-1.96) - \Phi(=1.96) \\ = .95 \end{align*}\]
Em que \(\Phi(x)\) representa a probabilidade de observar um valor menor ou igual que \(x\) na distrinbuição normal padrão. Como a probabilidade de observar um valor menor ou igual que \(1.96\) é \(97.5\%\), e a probabilidade de observar um valor menor que \(-1.96\) é \(2.5\%\), temos o resultado de \(95\%\) de confiança usual.
11.2 T-student
O problema é que nós não sabemos o valor de \(\sigma^2\). A gente pode tentar substituir \(\sigma^2\) por \(\hat{\sigma}^2\), o estimador da variância. Um estimador da variância é dado pela soma dos resíduos ao quadrado (já que a média é zero) dividido pelo \(n\).
\[ \hat{\sigma}^2 = \frac{\sum_{i=1}^n (Y_i - \hat{\alpha} - \hat{\beta} x_i)^2}{n} \]
Esse estimador é viesado e normalmente dividimos por \(n-2\), que são os chamados graus de liberdade: \(\frac{\sum_{i=1}^{n}\hat{e}_i^2}{n-2}\).
Esta maneira de explicar graus de liberdade, embora intuitiva, é errada. Como disse Rachael Meager no Twitter uma vez, ” I know enough to know it [degrees of freedom] can’t be ‘N minus number of parameters’ because once you do hierarchical/shrinkage it’s actually a substantively subtle and challenging task to ‘count’ how many parameters you have” 2. Eu não vou expandir muito aqui porque a definição correta requeriria conhecimento avançado de Álgebra Linear, mas basta dizer que o que ela está falando tem a ver com o fato de que em modelos multiníveis Bayesianos (por exemplo), o número de parâmetros não é facilmente determinado, de forma que essa fórmula de número de observações menos o número de parâmetros falha nesses e em outros casos (como modelos com regularização etc.).
De todo modo, para nós importa que, substituindo meu estimador não-viesado para a variância em nossa fórmula, temos:
\[ z^* = \frac{\hat{\beta} - \beta}{\sqrt{\frac{\hat{\sigma^2}}{(n -2) \cdot S^2_x}}} \] Lmebrando que:
\[ \hat{se}(\hat{\beta}) = \sqrt{\frac{\hat{\sigma}^2}{n - 2 \cdot S^2_x}} = \frac{\hat{\sigma}}{S_x \sqrt{n - 2 }} \]
E essa estatística de teste não é mais normalmente distribuída. Na verdade, é possível mostrar que ela na verdade segue uma distribuição t-Student com \(n-2\) graus de liberdade, usando a distribuição qui-quadrado na derivação.
11.2.1 Avançado - Derivação da t- de student
Comcemos com algumas preliminares.
Se \(Z_1, Z_2, \cdots, Z_d \sim N(0,1)\) são independentes, então definimos a distribuição Qui-quadrado de tal forma que: \(\chi^2_{d} = \sum_{i=1}^d Z_i^2\)
Se \(Z \sim N(0,1)\), então (pela definição acima). \(Z^2 \sim \chi^2_{1}\)
Lemrbando que a soma dos erros tem média zero, então: \(e_i - \mathbb{E}[e] = e_i\) e \(\frac{e_i}{\sqrt{Var(e_i)}} = \frac{e_i}{\sigma} \sim N(0,1)\)
Disso segue que: \[ \sum_{i=1}^n \frac{e_i^2}{\sigma^2} = \sum_{i=1}^n (\frac{e_i}{\sigma})^2 \sim \chi^2_{n} \] Como porém só temos \(n-2\) graus de liberdade, só temos \(n-2\) erros verdadeiramente independentes, então só podemos somar até \(n-2\), o que dá a ^2_{n-2}.
Por fim: Se \(Z \sim N(0,1)\), \(S^2 \sim \chi^2_d\) e \(Z\) e \(S^2\) são independentes, então:
\[ \frac{Z}{\sqrt{S^2/d}} \sim t_d \]
\[\begin{align} \frac{\hat{\beta} - \beta}{\hat{se}(\hat{\beta})} = \frac{\hat{\beta} - \beta}{\sigma} \times \frac{\sigma}{\hat{se}(\hat{\beta})} \\ = \frac{\frac{\hat{\beta} - \beta}{\sigma}}{\frac{\hat{se}(\hat{\beta})}{\sigma}} = \frac{N(0,1/ns^2_x)}{\frac{\hat{se}(\hat{\beta})}{\sigma}} = \frac{N(0,1/ns^2_x)}{\frac{\hat{\sigma}}{\sigma S_x\sqrt{n-2}}}\\ = \frac{S_x \times N(0,1/ns^2_x)}{\frac{\hat{\sigma}}{\sigma \sqrt{n-2}}} = \frac{N(0,1/n)}{\frac{\hat{\sigma}}{\sigma \sqrt{n-2}}} = \\ = \frac{\sqrt{n} \times N(0,1/n)}{\frac{\sqrt{n} \times \hat{\sigma}}{\sigma \sqrt{n-2}}} = \frac{N(0,1)}{\frac{\sqrt{n\hat{\sigma}^2}}{\sqrt{\sigma^2 \times (n-2)}}} \\ = \frac{N(0,1)}{\sqrt{\frac{n\hat{\sigma}^2}{\sigma^2 \times (n-2)}}} \\ = \frac{N(0,1)}{\sqrt{\chi^2_{n-2}/(n-2)}} \sim t_d \end{align}\]
No penúltimo passo, usamos de maneira um pouco “picareta” que se \(sum_{i=1}^n (\frac{e_i}{\sigma})^2 \sim \chi^2_{n}\), “então” eu posso aproximar numerador por \(\sum_{i=1}^n e_i^2\) por \(n\hat{\sigma}^2\), usando o fato de que a média é zero, e portanto ali é a variancia.
Digo que é “picareta” porque o erros não são a mesma coisa que os resíduos. Mas a matemática para fazer a prova correta está além dos nosso conhecimentos.
11.3 Teste de Hipótese e IC
Como consequência, podemos derivar o seguinte, para qualquer \(k >0\)
\[\begin{align*} \mathrm{P}(\beta - k \cdot \hat{se}[\hat{\beta}] \le \hat{\beta} \le \beta + k \cdot \hat{se}[\hat{\beta}] ) \\ = \mathrm{P}( -k \cdot \hat{se}[\hat{\beta}] \le \hat{\beta} - \beta \le k \cdot \hat{se}[\hat{\beta}] ) \\ = \mathrm{P}( -k \le \frac{\hat{\beta} - \beta}{\hat{se}[\hat{\beta}]} \le k ) \\ = t_{n-2}(k) \end{align*}\]
Em que, com um grande abuso de notação, estou chamando $ t_{n-2}(k)$ a probabilidade, na distribuição \(t\) de student com \(n-2\) graus de liberdade, de \(\hat{\beta}\) estar no intervalo \(-k, k\).
Se eu definir um nível de significância \(\alpha\) entre \(0\) e \(1\), sempre exisitrá um \(k\) que que a equação acima seja verdadeira.
## [1] -2.262157## [1] 2.262157## [1] -0.7027221## [1] 0.7027221Vamos então definir o intervalo amostral para \(\hat{\beta}\) como: \([\beta - k(n,\alpha)\hat{se}(\hat{\beta}),\beta + k(n,\alpha)\hat{se}(\hat{\beta})]\), ou seja, se a verdadeira inclinação da reta é \(\beta\), então meu \(\hat{\beta}\) estará nesse intervalo com probabilidade \(1 - \alpha\). O que nos leva ao teste de hipóte nulo de que \(\beta = \beta^*\), em particular, de que \(\beta^* = 0\), mas não precisa ser essa hipótese nula. E rejeitamos a nula se meu estimador está fora dese intervalo \([\beta^* - k(n,\alpha)\hat{se}(\hat{\beta}),\beta^* + k(n,\alpha)\hat{se}(\hat{\beta})]\), e aceitamos a nula se ele está no intervalo.
11.4 Propriedades Assintóticas
O que acontece à medida que \(n\) cresce? Como exercício, faça uma simulação no R, aumentando o \(n\) e verificando como fica o histograma da t de student.
11.5 Inferência Preditiva
É muito comum que queiramos fazer inferência para nossas previsões, isto é, quantificar a incerteza de nossas previsões da amostra para a população. Vamos retomar o modelo preditivo para eleições como exemplo. Vamos carregar os dados de 2018, que usamos para estimar um modelo preditivo, e vamos utilizar o modelo para prever o resultado de 2022. Como o TSE disponibilizou os dados por Zona eleitoral, vou utilizá-la como unidade (em vez de seção) para as observações.
Peguem os dados desse link. Baixem, descompactem e salvem na pasta onde o R aponta.
library(data.table)
library(tidyverse)
library(janitor)
library(tidyr)
# lista o nome do arquivo em csv
# unzip(here("dados", "votacao_secao_2018_BR.zip"), list = TRUE)
#read data1.csv into data frame
presid_18 <- fread(here("dados","votacao_secao_2018_BR.csv"), encoding = "Latin-1")
# Supondo que seu dataframe seja chamado df
df_resultados <- presid_18 %>%
dplyr::filter(!NR_VOTAVEL %in% c(95,96)) %>%
group_by(NR_ZONA, CD_MUNICIPIO, SG_UF, NR_VOTAVEL, NR_TURNO) %>%
summarise(total_votos = sum(QT_VOTOS)) %>%
pivot_wider(names_from = NR_TURNO, values_from = total_votos, values_fill = 0) %>%
janitor::clean_names() %>%
group_by(nr_zona, cd_municipio, sg_uf) %>%
mutate(total_validos_1t = sum(x1),
total_validos_2t = sum(x2)) %>%
dplyr::filter(nr_votavel == 17) %>%
mutate(percentual_bolso_1t = x1 /total_validos_1t ,
percentual_bolso_2t = x2 / total_validos_2t)
# remove
# rm(presid_18)
# modelo de regressão
reg1 <- lm(percentual_bolso_2t ~ percentual_bolso_1t, data = df_resultados)
summary(reg1)##
## Call:
## lm(formula = percentual_bolso_2t ~ percentual_bolso_1t, data = df_resultados)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.189870 -0.022821 -0.004147 0.018858 0.311149
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.019864 0.001058 18.78 <2e-16 ***
## percentual_bolso_1t 1.152802 0.002387 483.02 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.03557 on 6238 degrees of freedom
## Multiple R-squared: 0.974, Adjusted R-squared: 0.974
## F-statistic: 2.333e+05 on 1 and 6238 DF, p-value: < 2.2e-16df_resultados %>%
ggplot(aes(x=percentual_bolso_1t, y=percentual_bolso_2t)) + geom_point() +
geom_abline(slope = coef(reg1)[2] , intercept = coef(reg1)[1], colour = "blue")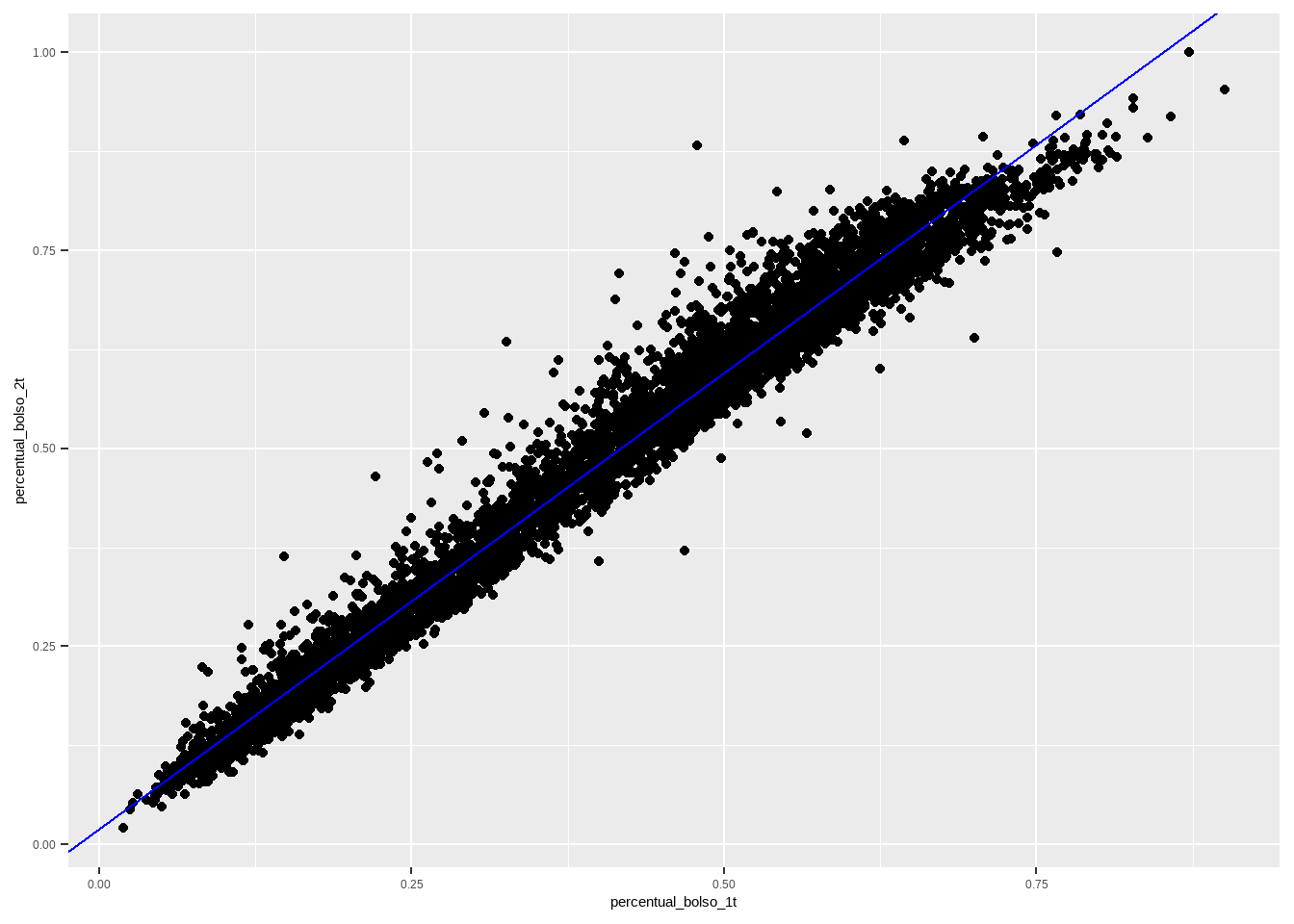
# dados de 2022
#read into data frame
presid_22 <- fread(here("dados","votacao_secao_2022_BR.csv"), encoding = "Latin-1")
df_resultados_22 <- presid_22 %>%
dplyr::filter(!NR_VOTAVEL %in% c(95,96)) %>%
group_by(NR_ZONA, CD_MUNICIPIO, SG_UF, NR_VOTAVEL, NR_TURNO) %>%
summarise(total_votos = sum(QT_VOTOS)) %>%
pivot_wider(names_from = NR_TURNO, values_from = total_votos, values_fill = 0) %>%
janitor::clean_names() %>%
group_by(nr_zona, cd_municipio, sg_uf) %>%
mutate(total_validos_1t = sum(x1),
total_validos_2t = sum(x2)) %>%
dplyr::filter(nr_votavel == 22) %>%
dplyr::filter(total_validos_1t >0) %>%
mutate(percentual_bolso_1t = x1 /total_validos_1t ,
percentual_bolso_2t = x2 / total_validos_2t)Agora que importamos os dados de 22, podemos fazer nossa previsão, usando os resultados do primeiro turno.
df_resultados_22 <- df_resultados_22 %>%
mutate(y_prev_2t = coef(reg1)[1] + coef(reg1)[2]*percentual_bolso_1t,
validos_previsto = total_validos_1t*y_prev_2t)
# previsão do resultado eleitoral antes de observar apuração do 2t, supondo comparecimento igual ao 1t
df_resultados_22 %>%
ungroup() %>%
summarise(total_bolso = sum(validos_previsto),
total_valido_previsto = sum(total_validos_1t),
perc_previsto = total_bolso/total_valido_previsto)## # A tibble: 1 × 3
## total_bolso total_valido_previsto perc_previsto
## <dbl> <int> <dbl>
## 1 61224817. 118229715 0.518# previsão do resultado eleitoral com o comparecimento do 2o turno real
df_resultados_22 <- df_resultados_22 %>%
mutate(y_prev_2t_alt = coef(reg1)[1] + coef(reg1)[2]*percentual_bolso_1t,
validos_previsto_alt = total_validos_2t*y_prev_2t_alt)
df_resultados_22 %>%
ungroup() %>%
summarise(total_bolso = sum(validos_previsto_alt),
total_valido_previsto = sum(total_validos_2t),
perc_previsto = total_bolso/total_valido_previsto)## # A tibble: 1 × 3
## total_bolso total_valido_previsto perc_previsto
## <dbl> <int> <dbl>
## 1 61501668. 118552342 0.519#E incerteza nas previsões?
previsoes <- predict(reg1, newdata = df_resultados_22, interval = "prediction", level = .95) %>%
as.data.frame()
df_resultados_22 <- df_resultados_22 %>%
ungroup() %>%
mutate(prev_perc = previsoes$fit,
prev_perc_lower = previsoes$lwr,
prev_perc_upper = previsoes$upr,
validos_prev = total_validos_2t*prev_perc,
validos_prev_lower = total_validos_2t*prev_perc_lower,
validos_prev_upper = total_validos_2t*prev_perc_upper)
df_resultados_22 %>%
summarise(perc_previsto = sum(validos_prev)/sum(total_validos_2t),
perc_previsto_lower = sum(validos_prev_lower)/sum(total_validos_2t),
perc_previsto_upper = sum(validos_prev_upper)/sum(total_validos_2t))## # A tibble: 1 × 3
## perc_previsto perc_previsto_lower perc_previsto_upper
## <dbl> <dbl> <dbl>
## 1 0.519 0.449 0.589Como vimos, apenas com base nos dados do primeiro turno, ao nível da zona eleitoral, não era possível prever o resultado final. E à medida que os dados por zona eleitoral foram divulgados, podíamos melhorar nossa previsão de algum modo?
E será que se incluírmos mais variáveis, podemos melhorar o modelo? Vamos deixar isso para a próxima aula. Por enquanto, vamos fazer o seguinte exercício. Como nossas previsões iriam evoluir, com basse nesse modelo, à medida que acontecia a apuração?
see (if twitter is still availble to look at) https://twitter.com/economeager/status/1596450647599190017)↩︎